
Der Einfachheit halber wird die Rekursion zum Erstellen von Baumknoten verwendet. Obwohl die Rekursion keine perfekte Implementierung ist, ist sie zur Erklärung des Prinzips am intuitivsten.
Importieren Sie zuerst die Bibliothek
import pandas as pd import numpy as np import matplotlib.pyplot as plt
Zuerst müssen wir die Trainingsdaten erstellen. Unsere Daten haben eine unabhängige Variable (x) und eine korrelierte Variable (y) und verwenden Numpy, um Gaußsches Rauschen zu den korrelierten Werten hinzuzufügen mathematisch ausgedrückt als
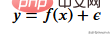
Hier ist Lärm. Der Code wird unten angezeigt.
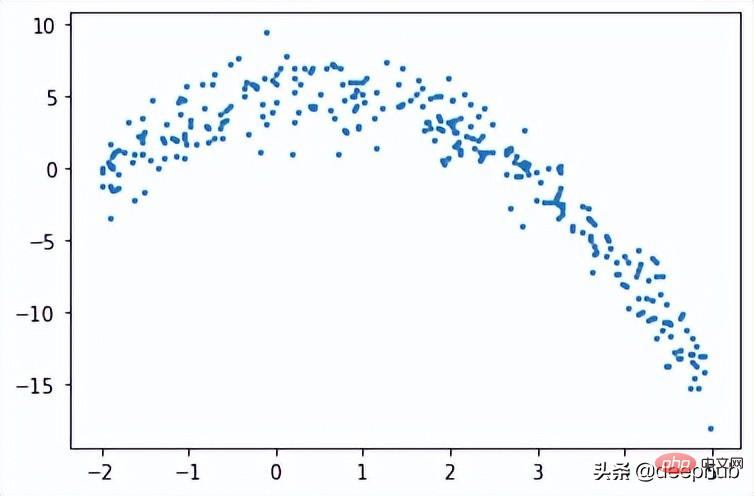
def f(x): mu, sigma = 0, 1.5 return -x**2 + x + 5 + np.random.normal(mu, sigma, 1) num_points = 300 np.random.seed(1) x = np.random.uniform(-2, 5, num_points) y = np.array( [f(i) for i in x] ) plt.scatter(x, y, s = 5)
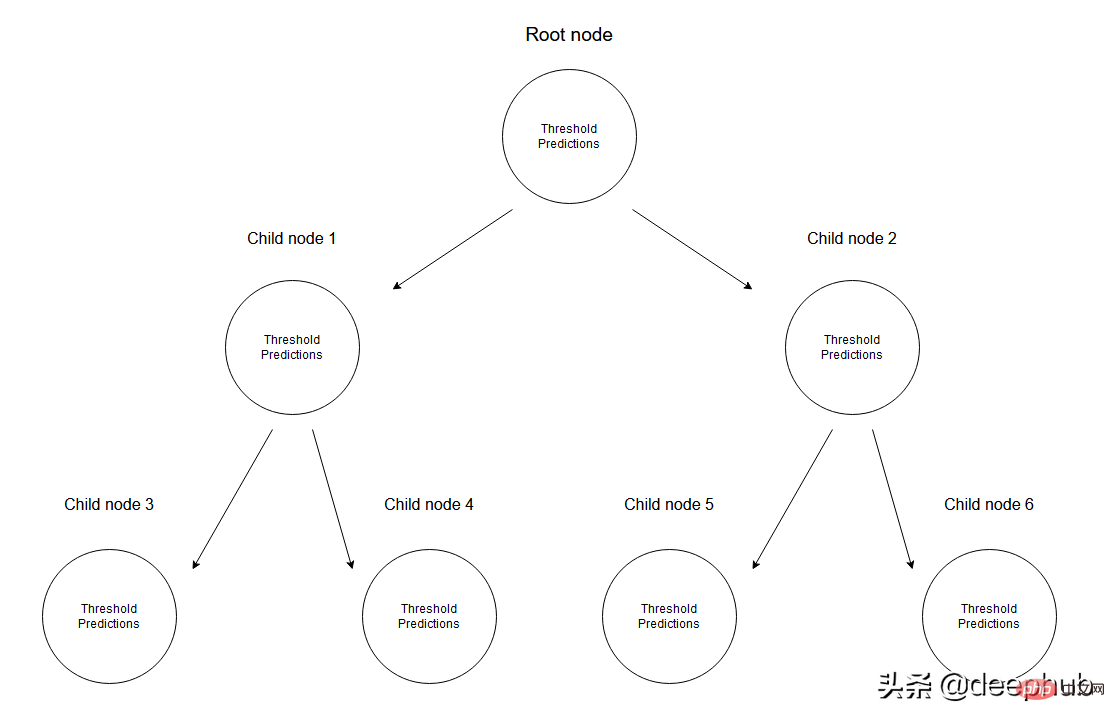
In einem Regressionsbaum werden numerische Daten vorhergesagt, indem ein Baum aus mehreren Knoten erstellt wird. Die folgende Abbildung zeigt ein Beispiel für die Baumstruktur eines Regressionsbaums, bei dem jeder Knoten seinen eigenen Schwellenwert hat, der zum Teilen der Daten verwendet wird.
Bei einem gegebenen Datensatz erreichen die Eingabewerte die Blattknoten über die entsprechenden Spezifikationen. Alle Eingabewerte, die Knoten M erreichen, können durch Teilmengen von X dargestellt werden. Lassen Sie uns diese Situation mathematisch durch eine Funktion ausdrücken, die 1 ergibt, wenn ein gegebener Eingabewert den Knoten M erreicht, und andernfalls 0.
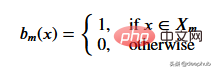
Finden Sie den Schwellenwert, der die Daten aufteilt: Iterieren Sie über die Trainingsdaten, indem Sie bei jedem Schritt zwei aufeinanderfolgende Punkte auswählen und deren Durchschnitt berechnen. Der berechnete Mittelwert teilt die Daten in zwei Schwellenwerte auf.
Betrachten wir zunächst zufällige Schwellenwerte, um eine bestimmte Situation zu veranschaulichen.
threshold = 1.5 low = np.take(y, np.where(x < threshold)) high = np.take(y, np.where(x > threshold)) plt.scatter(x, y, s = 5, label = 'Data') plt.plot([threshold]*2, [-16, 10], 'b--', label = 'Threshold line') plt.plot([-2, threshold], [low.mean()]*2, 'r--', label = 'Left child prediction line') plt.plot([threshold, 5], [high.mean()]*2, 'r--', label = 'Right child prediction line') plt.plot([-2, 5], [y.mean()]*2, 'g--', label = 'Node prediction line') plt.legend()

Die blaue vertikale Linie stellt einen einzelnen Schwellenwert dar, von dem wir annehmen, dass er der Mittelwert zweier beliebiger Punkte ist und später zum Teilen der Daten verwendet wird.
Unsere erste Vorhersage für dieses Problem ist der Durchschnitt (grüne horizontale Linie) aller Trainingsdaten (y-Achse). Und die beiden roten Linien sind die Vorhersagen der zu erstellenden untergeordneten Knoten.
Es ist offensichtlich, dass keiner dieser Durchschnittswerte unsere Daten gut darstellt, aber ihre Unterschiede sind auch offensichtlich: Die Master-Knoten-Vorhersage (grüne Linie) erhält den Mittelwert aller Trainingsdaten, die wir in zwei untergeordnete Knoten aufteilen, die wiederum zwei untergeordnete Knoten haben ihre eigenen Vorhersagen (rote Linie). Im Vergleich zur grünen Linie stellen diese beiden untergeordneten Knoten ihre entsprechenden Trainingsdaten besser dar. Ein Regressionsbaum teilt die Daten kontinuierlich in zwei Teile auf und erstellt aus jedem Knoten zwei untergeordnete Knoten, bis ein bestimmter Stoppwert erreicht ist (das ist die Mindestdatenmenge, die ein Knoten haben kann). Dadurch wird der Baumbildungsprozess frühzeitig gestoppt, was wir als vorgeschnittenen Baum bezeichnen.
Warum gibt es einen Frühstoppmechanismus? Wenn wir mit der Zuweisung fortfahren würden, bis ein Knoten nur noch einen Wert hat, entsteht ein Überanpassungsszenario, in dem alle Trainingsdaten nur sich selbst vorhersagen können.
Hinweis: Wenn das Modell vollständig ist, werden weder der Wurzelknoten noch irgendwelche Zwischenknoten zur Vorhersage von Werten verwendet, sondern die Blätter des Regressionsbaums (der der letzte Knoten des Baums sein wird) zur Vorhersage.
Um den Schwellenwert zu erhalten, der die gegebenen Schwellenwertdaten am besten repräsentiert, verwenden wir die Restquadratsumme. Es kann mathematisch definiert werden als
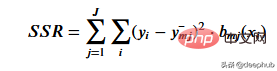
Mal sehen, wie dieser Schritt funktioniert.
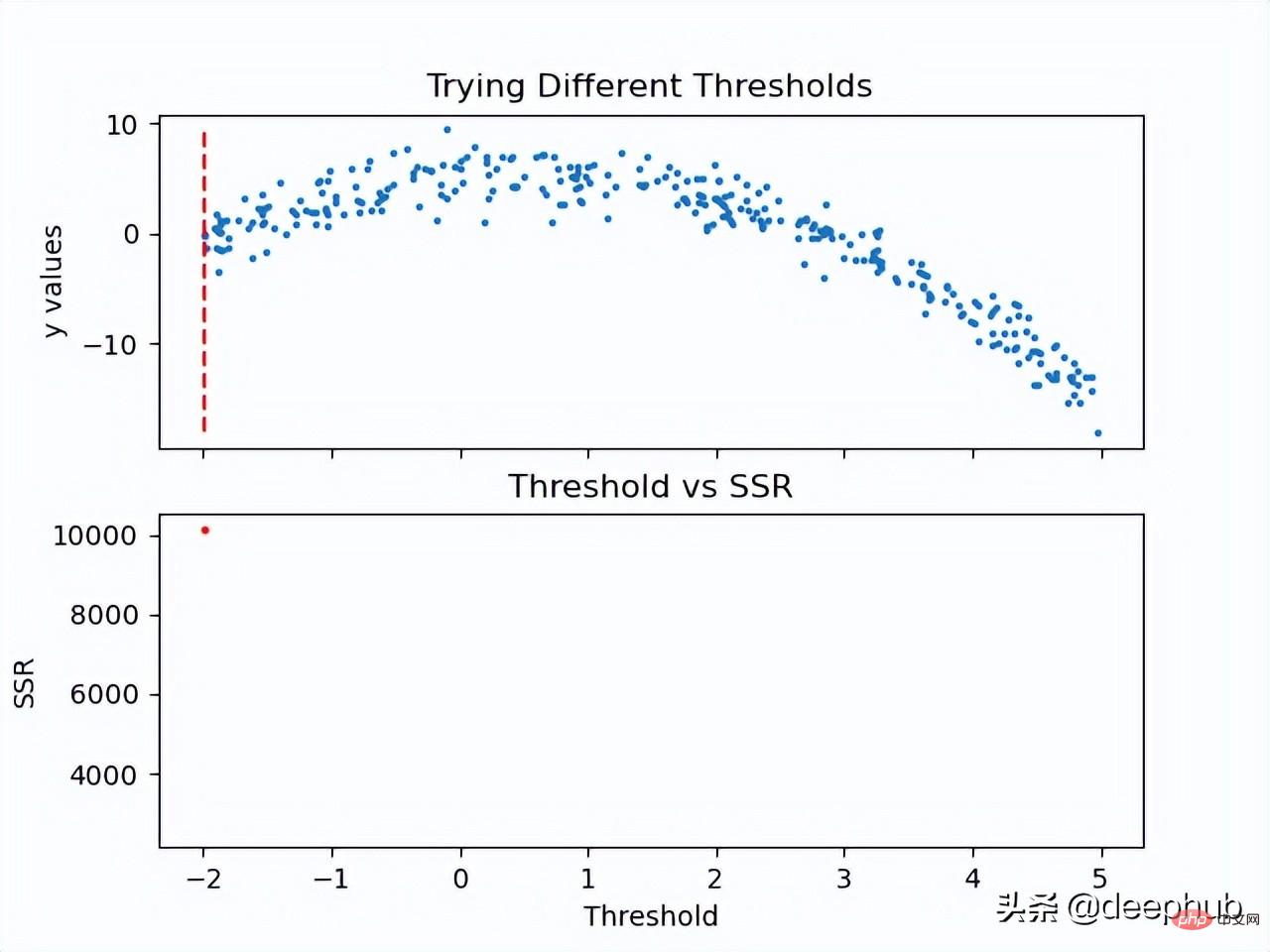
Da nun der SSR-Wert des Schwellenwerts berechnet ist, kann der Schwellenwert mit dem minimalen SSR-Wert übernommen werden. Verwenden Sie diesen Schwellenwert, um die Trainingsdaten in zwei Teile aufzuteilen (niedriger und hoher Teil), wobei der niedrige Teil zum Erstellen des linken untergeordneten Knotens und der hohe Teil zum Erstellen des rechten untergeordneten Knotens verwendet wird.
def SSR(r, y):
return np.sum( (r - y)**2 )
SSRs, thresholds = [], []
for i in range(len(x) - 1):
threshold = x[i:i+2].mean()
low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))
guess_low = low.mean()
guess_high = high.mean()
SSRs.append(SSR(low, guess_low) + SSR(high, guess_high))
thresholds.append(threshold)
print('Minimum residual is: {:.2f}'.format(min(SSRs)))
print('Corresponding threshold value is: {:.4f}'.format(thresholds[SSRs.index(min(SSRs))]))
在进入下一步之前,我将使用pandas创建一个df,并创建一个用于寻找最佳阈值的方法。所有这些步骤都可以在没有pandas的情况下完成,这里使用他是因为比较方便。
df = pd.DataFrame(zip(x, y.squeeze()), columns = ['x', 'y']) def find_threshold(df, plot = False): SSRs, thresholds = [], [] for i in range(len(df) - 1): threshold = df.x[i:i+2].mean() low = df[(df.x <= threshold)] high = df[(df.x > threshold)] guess_low = low.y.mean() guess_high = high.y.mean() SSRs.append(SSR(low.y.to_numpy(), guess_low) + SSR(high.y.to_numpy(), guess_high)) thresholds.append(threshold) if plot: plt.scatter(thresholds, SSRs, s = 3) plt.show() return thresholds[SSRs.index(min(SSRs))]
在将数据分成两个部分后就可以为低值和高值找到单独的阈值。需要注意的是这里要增加一个停止条件;因为对于每个节点,属于该节点的数据集中的点会变少,所以我们为每个节点定义了最小数据点数量。如果不这样做,每个节点将只使用一个训练值进行预测,会导致过拟合。
可以递归地创建节点,我们定义了一个名为TreeNode的类,它将存储节点应该存储的每一个值。使用这个类我们首先创建根,同时计算它的阈值和预测值。然后递归地创建它的子节点,其中每个子节点类都存储在父类的left或right属性中。
在下面的create_nodes方法中,首先将给定的df分成两部分。然后检查是否有足够的数据单独创建左右节点。如果(对于其中任何一个)有足够的数据点,我们计算阈值并使用它创建一个子节点,用这个新节点作为树再次调用create_nodes方法。
class TreeNode(): def __init__(self, threshold, pred): self.threshold = threshold self.pred = pred self.left = None self.right = None def create_nodes(tree, df, stop): low = df[df.x <= tree.threshold] high = df[df.x > tree.threshold] if len(low) > stop: threshold = find_threshold(low) tree.left = TreeNode(threshold, low.y.mean()) create_nodes(tree.left, low, stop) if len(high) > stop: threshold = find_threshold(high) tree.right = TreeNode(threshold, high.y.mean()) create_nodes(tree.right, high, stop) threshold = find_threshold(df) tree = TreeNode(threshold, df.y.mean()) create_nodes(tree, df, 5)
这个方法在第一棵树上进行了修改,因为它不需要返回任何东西。虽然递归函数通常不是这样写的(不返回),但因为不需要返回值,所以当没有激活if语句时,不做任何操作。
在完成后可以检查此树结构,查看它是否创建了一些可以拟合数据的节点。 这里将手动选择第一个节点及其对根阈值的预测。
plt.scatter(x, y, s = 0.5, label = 'Data') plt.plot([tree.threshold]*2, [-16, 10], 'r--', label = 'Root threshold') plt.plot([tree.right.threshold]*2, [-16, 10], 'g--', label = 'Right node threshold') plt.plot([tree.threshold, tree.right.threshold], [tree.right.left.pred]*2, 'g', label = 'Right node prediction') plt.plot([tree.left.threshold]*2, [-16, 10], 'm--', label = 'Left node threshold') plt.plot([tree.left.threshold, tree.threshold], [tree.left.right.pred]*2, 'm', label = 'Left node prediction') plt.plot([tree.left.left.threshold]*2, [-16, 10], 'k--', label = 'Second Left node threshold') plt.legend()
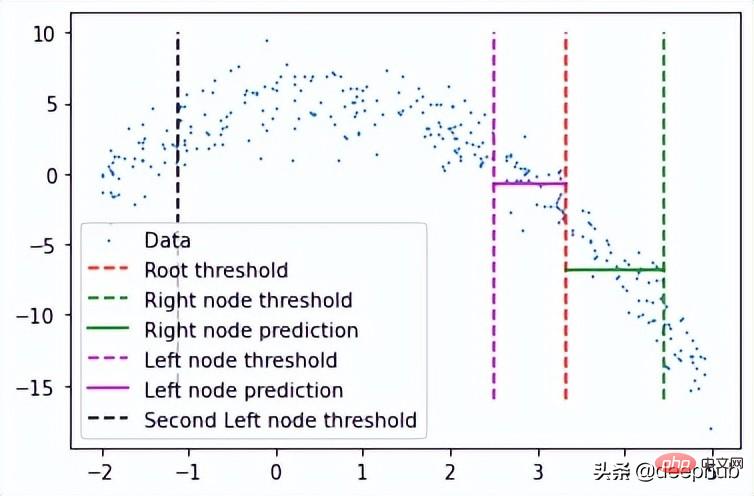
这里看到了两个预测:
这里我手动剪切了预测线的宽度,因为如果给定的x值达到了这些节点中的任何一个,则将以属于该节点的所有x值的平均值表示,这也意味着没有其他x值参与 在该节点的预测中(希望有意义)。
这种树形结构远不止两个节点那么简单,所以我们可以通过如下调用它的子节点来检查一个特定的叶子节点。
tree.left.right.left.left
这当然意味着这里有一个向下4个子结点长的分支,但它可以在树的另一个分支上深入得多。
我们可以创建一个预测方法来预测任何给定的值。
def predict(x): curr_node = tree result = None while True: if x <= curr_node.threshold: if curr_node.left: curr_node = curr_node.left else: break elif x > curr_node.threshold: if curr_node.right: curr_node = curr_node.right else: break return curr_node.pred
预测方法做的是沿着树向下,通过比较我们的输入和每个叶子的阈值。如果输入值大于阈值,则转到右叶,如果小于阈值,则转到左叶,以此类推,直到到达任何底部叶子节点。然后使用该节点自身的预测值进行预测,并与其阈值进行最后的比较。
使用x = 3进行测试(在创建数据时,可以使用上面所写的函数计算实际值。-3**2+3+5 = -1,这是期望值),我们得到:
predict(3) # -1.23741
这里用相对平方误差验证数据
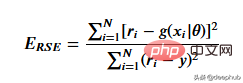
def RSE(y, g):
return sum(np.square(y - g)) / sum(np.square(y - 1 / len(y)*sum(y)))
x_val = np.random.uniform(-2, 5, 50)
y_val = np.array( [f(i) for i in x_val] ).squeeze()
tr_preds = np.array( [predict(i) for i in df.x] )
val_preds = np.array( [predict(i) for i in x_val] )
print('Training error: {:.4f}'.format(RSE(df.y, tr_preds)))
print('Validation error: {:.4f}'.format(RSE(y_val, val_preds)))可以看到误差并不大,结果如下


一个更适合回归树模型的数据:因为我们的数据是多项式生成的数据,所以使用多项式回归模型可以更好地拟合。我们更换一下训练数据,把新函数设为
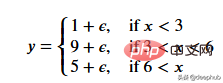
def f(x): mu, sigma = 0, 0.5 if x < 3: return 1 + np.random.normal(mu, sigma, 1) elif x >= 3 and x < 6: return 9 + np.random.normal(mu, sigma, 1) elif x >= 6: return 5 + np.random.normal(mu, sigma, 1) np.random.seed(1) x = np.random.uniform(0, 10, num_points) y = np.array( [f(i) for i in x] ) plt.scatter(x, y, s = 5)
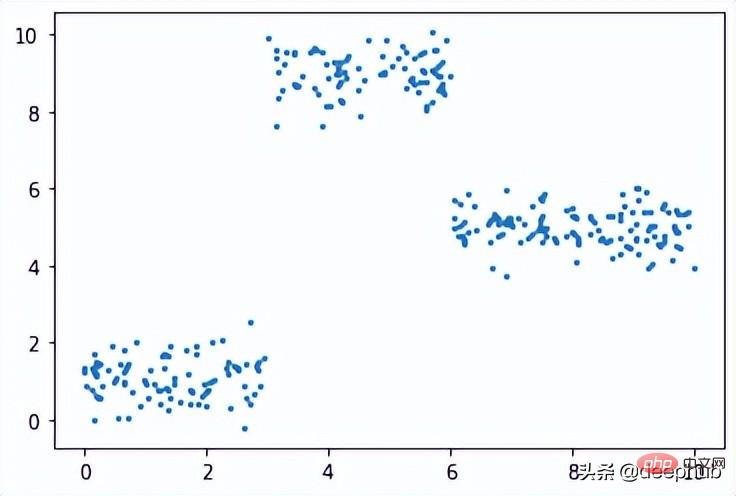
在此数据集上运行了上面的所有相同过程,结果如下
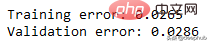
比我们从多项式数据中获得的误差低。
最后共享一下上面动图的代码:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
#===================================================Create Data
def f(x):
mu, sigma = 0, 1.5
return -x**2 + x + 5 + np.random.normal(mu, sigma, 1)
np.random.seed(1)
x = np.random.uniform(-2, 5, 300)
y = np.array( [f(i) for i in x] )
p = x.argsort()
x = x[p]
y = y[p]
#===================================================Calculate Thresholds
def SSR(r, y): #send numpy array
return np.sum( (r - y)**2 )
SSRs, thresholds = [], []
for i in range(len(x) - 1):
threshold = x[i:i+2].mean()
low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))
guess_low = low.mean()
guess_high = high.mean()
SSRs.append(SSR(low, guess_low) + SSR(high, guess_high))
thresholds.append(threshold)
#===================================================Animated Plot
fig, (ax1, ax2) = plt.subplots(2,1, sharex = True)
x_data, y_data = [], []
x_data2, y_data2 = [], []
ln, = ax1.plot([], [], 'r--')
ln2, = ax2.plot(thresholds, SSRs, 'ro', markersize = 2)
line = [ln, ln2]
def init():
ax1.scatter(x, y, s = 3)
ax1.title.set_text('Trying Different Thresholds')
ax2.title.set_text('Threshold vs SSR')
ax1.set_ylabel('y values')
ax2.set_xlabel('Threshold')
ax2.set_ylabel('SSR')
return line
def update(frame):
x_data = [x[frame:frame+2].mean()] * 2
y_data = [min(y), max(y)]
line[0].set_data(x_data, y_data)
x_data2.append(thresholds[frame])
y_data2.append(SSRs[frame])
line[1].set_data(x_data2, y_data2)
return line
ani = FuncAnimation(fig, update, frames = 298,
init_func = init, blit = True)
plt.show()Das obige ist der detaillierte Inhalt vonHandschriftliche Regressionsbäume von Grund auf mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




