lineare Zeitauswahl-häufiges Problem-php.cn

lineare Zeitauswahl

Definition: Gegeben n Elemente in einer linearen Folge und eine ganze Zahl k, 1≤k≤n, ist es erforderlich, das k-kleinste unter diesen n Elementen zu finden Elemente.

(1) In einigen Sonderfällen ist es einfach, einen linearen Zeitalgorithmus zu entwerfen, um das Auswahlproblem zu lösen. Wenn Sie beispielsweise das größte oder kleinste Element auswählen möchten, kann dies natürlich in O(n)-Zeit erfolgen. (Nur ein Vergleich)

(2) Das allgemeine Auswahlproblem, insbesondere das Auswahlproblem des Medians, scheint schwieriger zu sein als das kleinste (große) Element. Tatsächlich sind sie jedoch im Sinne der asymptotischen Ordnung gleich. Dies kann auch in O(n)-Zeit erfolgen.

Lineare Zeitauswahlmethode eins: randomizedSelect

Idee: Zufällige Schnellsortierung anpassen, anstatt das gesamte Array zu sortieren, aber die ausgewählte Sortierung ( Schneller)

Zeitkomplexität:

(1) Im schlimmsten Fall benötigt der Algorithmus randomizedSelect O(n^2) Berechnungszeit

z . Wir müssen das kleinste Element finden, aber die Position, die wir bei jeder Division durch die Partitionsfunktion erhalten, ist immer sehr groß (nahe bei n) (das heißt, sie wird immer am größten Element geteilt)

( 2) aber es kann Es ist bewiesen, dass der Algorithmus randomizedSelect das k-kleinste Element unter n Eingabeelementen in der durchschnittlichen Zeit von O(n) finden kann.

Der Code lautet wie folgt:

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int Partition(int a[],int p,int r){
    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int RandomizedPartition(int a[],int p,int r){
    int i=rand()%(r-p)+p;
    swap(a[p],a[i]);
    return Partition(a,p,r);
}

int RandomizedSelect(int a[],int p,int r,int k){
    if(p==r)return a[p];
    int i=RandomizedPartition(a,p,r);//返回基准元素的位置
    int j=i-p+1;//表示基准元素及其左边一共多少个元素
    if(k<=j)RandomizedSelect(a,p,i,k);
    else RandomizedSelect(a,i+1,r,k-j);
}
int main(){
    int a[10]={3,1,7,6,5,9,8,2,0,4};
    int x;
    while(scanf("%d",&x)!=EOF){
        int ans=RandomizedSelect(a,0,9,x);
        printf("%d\n",ans);
    }
}

Nach dem Login kopieren

Lineare Zeitauswahlmethode zwei:

Wenn Sie a<🎜 in linearer Zeit finden können >Teilungsbasis, sodass die Länge der beiden gemäß dieser Basis geteilten Unterarrays mindestens das ε-fache der Länge des ursprünglichen Arrays beträgt (0<ε<1 ist eine bestimmte positive Konstante). Es kann im schlimmsten Fall verwendet werden. Es dauert O(n) Zeit, die Auswahlaufgabe abzuschließen.

Wenn beispielsweise ε=9/10, wird die Länge des durch den rekursiven Aufruf des Algorithmus erzeugten Subarrays um mindestens 1/10 verkürzt. Daher erfüllt die vom Algorithmus benötigte Berechnungszeit T(n) im schlimmsten Fall die rekursive Formel T(n)≤T(9n/10)+O(n). Daraus können wir T(n)=O(n) erhalten.

Als der Lehrer darüber sprach, betonte er, dass „finden“ und nicht „finden“ bedeutet, den Median zu finden Wir wollen den Wert und unsere vorherige Schnellsortierung usw. bestanden darin, die Position des Werts zu bestimmen, das heißt, das Referenzelement an der richtigen Position zu platzieren.

Schritte:

(1) Teilen Sie n Eingabeelemente jeweils in n/5 (aufgerundete) Gruppen auf Die Gruppe enthält 5 Elemente, und es kann höchstens eine Gruppe geben, die nicht 5 Elemente enthält. Verwenden Sie einen beliebigen Sortieralgorithmus, um die Elemente in jeder Gruppe zu sortieren und den Median jeder Gruppe zu ermitteln, insgesamt n/5 (aufgerundet).

(2) Rufen Sie rekursiv „select“ auf, um den Median dieser

n/5 (aufgerundet) Elemente zu ermitteln. Wenn n/5 (aufgerundet)

eine gerade Zahl ist, ermitteln Sie den größeren ihrer beiden Mediane. Verwenden Sie dieses Element als Grundlage für die Division.

Schematische Darstellung der Partitionierungsstrategie:

Weißer Punkt: Median jeder Gruppe; Punkt x: Median des Medians

Beispiel: 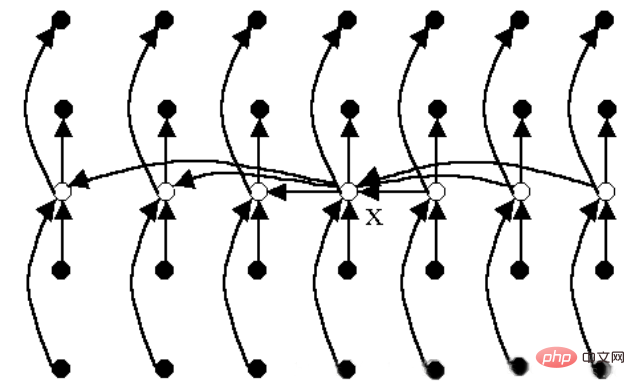lineare Zeitauswahl

Suchen Sie in aufsteigender Reihenfolge das folgende Das 18. Element von 29 Elemente: 8,31,60,33,17,4,51,57,49,35,11,43,37,3,13,52,6,19,25,32, 54,16,5,41,7,23,22,46,29.(1) Teilen Sie die ersten 25 Elemente in 5 (=floor(29/5)) Gruppen: (8,31,60, 33 ,17),(4,51,57,49,35),(11,43,37,3,13),(52,6,19,25,32),(54,16,5,41, 7 );(2) Extrahieren Sie das Medianelement jeder Gruppe, um die Menge {31,49,13,25,16} zu bilden;(3) Verwenden Sie den Algorithmus rekursiv, um den Median der Menge zu ermitteln, Erhalten m=25;

(4) Teilen Sie die 29 Elemente gemäß m=25 in 3 Unterarrays (in der ursprünglichen Reihenfolge)

P={8,17,4,11, 3,13,6 ,19 ,16,5,7,23,22}
Q={25}

R={31,60,33,51,57,49,35,43,37,52, 32, 54,41,46,29}

(5) Da |P|=13,|Q|=1,k=18, also P und Q aufgeben und k=18-13-1 = machen 4, führe diesen Algorithmus rekursiv auf R aus; 52},{32,54,41,46,29}
(7) Finden Sie das Medianelement dieser drei Gruppen von Elementen: {51,43,41}, das Medianelement dieser Menge ist 43;
(8) Teilen Sie R in 3 Gruppen basierend auf 43 auf:

{31, 33, 35,37,32, 41, 29},{43},{60, 51,57 , 49, 52, 54, 46}

Komplexität:

Angenommen, die Array-Länge beträgt n

Wenn n <75, beträgt die vom Algorithmus verwendete Berechnungszeit einen bestimmten Wert nicht Konstante C1

Wenn n≥75, wird die for-Schleife n/5-mal ausgeführt und benötigt jedes Mal eine bestimmte Konstante (eine feste Zahl soll unter 5 gesucht werden!); Die Länge beträgt 1/5 der ursprünglichen Länge. Die benötigte Zeit kann als T(n/5) aufgezeichnet werden. Nach der Teilung enthält das erhaltene Array höchstens 3n/4 Elemente und die benötigte Zeit wird als T(3n/4) aufgezeichnet ). T(n) kann also rekursiv ausgedrückt werden als:

Die Lösung für diesen rekursiven Ausdruck ist T(n)=O(n)

上述算法将每一组的大小定为5，并选取75作为是否作递归调用的分界点（大于75使用该算法）。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn，0<ε<1。这是使T(n)=O(n)的关键之处。当然，除了5和75之外，还有其他选择。

注意：

（1）设中位数的中位数是x，比x小和比x大的元素至少3*(n-5)/10个，原因：

3*(n/5-1)*1/2

3---中位数比x小的每一组中有3个元素比x小

n/5-1---有5个数的组数

1/2---大概有1/2组的中位数比x小

（2）而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4，也就是说，长度最长为原长度的3/4。

lineare Zeitauswahl

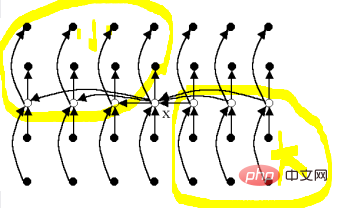
如图，划分的部分左上是肯定比x小的（大概占1/4）右下是肯定比x大的（大概占1/4）左下和右上不确定，就算这两部分同时不比x小或比x大，划分成的子区间也能至少缩短1/4!

核心代码：

Type Select(Type a[], int p, int r, int k)
{
      if (r-p<75) {
        //用某个简单排序算法对数组a[p:r]排序;
        return a[p+k-1];
        };
      for (int i=0;i<=(r-p-4)/5;i++)//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面
  
      //找中位数的中位数，r-p-4即上面所说的n-5
      Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//x是中位数的中位数
      int i=Partition(a,p,r,x),j=i-p+1;//i为快排一趟找到区间[p,r]中x应该在的位置，j为[p,i]区间的元素个数
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

Nach dem Login kopieren

关键的代码是：

for ( int i = 0; i<=(r-p-4)/5; i++ )//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面

Nach dem Login kopieren

一共(r-p+1)/5个组

注意这里i从0开始表示，为了方便交换时带入数组的下标，0-(r-p-4)/5，即一共(r-p-4)/5+1各组，即(r-p+1)/5个组

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
using namespace std;

void bubbleSort(int a[],int p,int r){
    for(int i=p;i<r;i++){
        for(int j=i+1;j<=r;j++){
            if(a[j]<a[i])swap(a[i],a[j]);
        }
    }
}

int Partition(int a[],int p,int r,int val){
    int pos;
    for(int q=p;q<=r;q++){
        if(a[q]==val){pos=q;break;}
    }
    swap(a[p],a[pos]);

    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int Select(int a[],int p,int r,int k){
    if(r-p<75){
        bubbleSort(a,p,r);
        return a[p+k-1];
    }

    for(int i=0;i<=(r-p-4)/5;i++){//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
        int s=p+5*i,t=s+4;
        for(int j=0;j<3;j++){//冒泡排序，从后开始排，结果使得后三个数是排好顺序的（递增）
            for(int n=s;n<t-j;n++){
                if(a[n]>a[n+1])swap(a[n],a[n-1]);
            }
        }
        swap(a[p+i],a[s+2]);//交换每组中的中位数到前面
    }
    //(r-p-4)/5表示组数-1，则[p,p+(r-p-4)/5]的区间长度等于组数
    int x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//求中位数的中位数
    int i=Partition(a,p,r,x),j=i-p+1;
    if(k<=j)return Select(a,p,i,k);
    else return Select(a,i+1,r,k-j);
}
int main(){
    int x;
    //数组a存了0-79
    int a[80]={3,1,7,6,5,9,8,2,0,4,
               13,11,17,16,15,19,18,12,10,14,
               23,21,27,26,25,29,28,22,20,24,
               33,31,37,36,35,39,38,32,30,34,
               43,41,47,46,45,49,48,42,40,44,
               53,51,57,56,55,59,58,52,50,54,
               63,61,67,66,65,69,68,62,60,64,
               73,71,77,76,75,79,78,72,70,74,
              };
    while(scanf("%d",&x)!=EOF){
        printf("第%d大的数是%d\n",x,Select(a,0,79,x));
    }
}

Nach dem Login kopieren

qwq，博主nc写错输出了，“第i小的数”

lineare Zeitauswahl

更多常见问题的相关技术文章，请访问常见问题教程栏目进行学习！

Das obige ist der detaillierte Inhalt vonlineare Zeitauswahl. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!