
Der Inhalt dieses Artikels befasst sich mit der Verwendung von Python zur Berechnung von Pi (Codebeispiel). Ich hoffe, dass er für Sie hilfreich ist.
1. Einführung in π
Einführung in π
Pi wird durch den griechischen Buchstaben π (ausgesprochen pài) dargestellt, der eine Konstante ist ( ungefähr gleich 3,141592654), was das Verhältnis von Umfang und Durchmesser eines Kreises darstellt. Es ist eine unendliche, sich nicht wiederholende Dezimalzahl. Im täglichen Leben wird 3,14 normalerweise zur Darstellung von Pi für Näherungsberechnungen verwendet.
Der Lösungsprozess von π
Im Jahr 1965 veröffentlichte der britische Mathematiker John Wallis eine mathematische Monographie, in der er eine Formel herleitete und feststellte, dass Pi gleich Unendlich ist. Das Produkt aus miteinander multiplizierten Brüchen.
Im Jahr 2015 entdeckten Wissenschaftler der Universität Rochester die gleiche Formel für Pi in quantenmechanischen Berechnungen der Energieniveaus von Wasserstoffatomen.
Am 14. März 2019 gab Google bekannt, dass Pi nun 31,4 Billionen Dezimalstellen erreicht hat.
Hier verwende ich eine Formel, die meiner Meinung nach „gut“ zu lösen ist. Gut, weil die Berechnungsergebnisse relativ genau sind, aber der Berechnungsprozess dauert lange ~~
2. Näherungsberechnung von π
1. Berechnungsformel
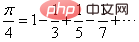
2. Methodenerklärung
Die Zähler auf der rechten Seite der Gleichung sind alle 1 und der Nenner Es ist eine aufsteigende Folge, beginnend mit dem ersten Element ist das Vorzeichen der ungeraden Terme positiv und das Vorzeichen der geraden Terme negativ. Je größer und kleiner der Nenner auf der rechten Seite der Gleichung ist, desto genauer ist der berechnete Wert von Pi. Anders ausgedrückt: Je mehr Terme auf der rechten Seite der Gleichung stehen, desto genauer ist der berechnete Wert.
3. Code-Implementierung (Python)
from math import fabs #导入数学模块
from time import perf_counter #导入时间模块
def Bar(i): #动态文本条
N = pow(10,level)
a = int((i/N)*50)
b = 50 - a
Y , N = '*' * a , '.' * b
print("\r计算中:{:3.0f}% [{}->{}] {:.2f}s"
.format(2*a,Y,N,perf_counter()),end='')
level = eval(input('计算Pi精确到小数点后几位数:'))
print('\n{:=^70}'.format('计算开始'))
a,b,pi,tmp = 1,1,0,1
i = 0
'''
a 分子 | b 分母 | pi 圆周率
tmp 存储a/b的值 | i 执行进度
'''
perf_counter() #开始计时
while (fabs(tmp) >= pow(10,-level)): #计算Pi
pi += tmp
b += 2
a = -a
tmp = a/b
i += 2
Bar(i) #调用函数,实时显示计算进度
print('\n{:=^70}'.format('计算完成'))
print('\nPi的计算值为:{}'.format(round(pi*4,level))) #输出计算结果4. Bildbeispiel
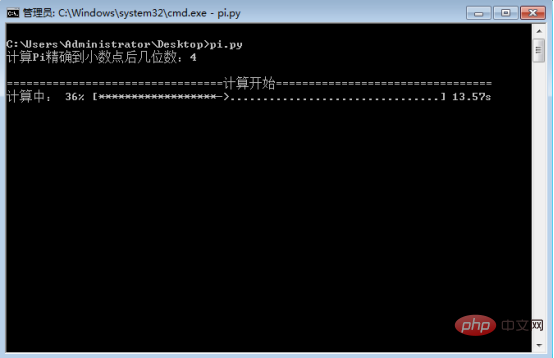

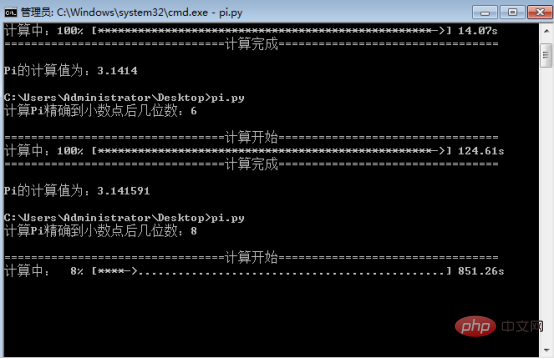
Wie aus den obigen drei Bildern ersichtlich ist, dauert es nur 14,07 Sekunden, um auf 4 Dezimalstellen genau zu sein, 124,61 Sekunden, um auf 6 Dezimalstellen genau zu sein, und 850 / 8 % = 10625, um genau zu sein auf 8 Dezimalstellen, was ungefähr 177 Minuten entspricht, was 2,95 Stunden entspricht. Diese Methode ist gut, aber die Berechnung dauert immer noch lange.
„Pi“ ist eine wunderbare und schöne Existenz. Es ist wie eine Art unvollkommene Schönheit, solange man die Augen hat, Schönheit zu entdecken.
Im Jahr 2011 gab die International Mathematical Association offiziell bekannt, dass der 14. März jedes Jahres der Internationale Tag der Mathematik sein wird. Die Quelle ist das Pi des alten chinesischen Mathematikers Zu Chongzhi.
Das obige ist der detaillierte Inhalt vonSo berechnen Sie Pi mit Python (Codebeispiel). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!