
Dieser Artikel stellt hauptsächlich die detaillierte Erklärung der Berechnung bestimmter Integrale mithilfe der Monte-Carlo-Methode in der Python-Programmierung vor. Er hat einen gewissen Referenzwert und Freunde in Not können sich darauf beziehen.
Ich glaube, damals, als ich die Postgraduierten-Aufnahmeprüfung ablegte, wünschte ich, ich wüsste, dass es so eine gute Sache gibt, bestimmte Integrale zu berechnen. . . Nur ein Scherz, die Berechnung bestimmter Integrale war damals nicht so einfach. Aber es brachte mich auf die Idee, Programmiersprachen zur Lösung komplexerer mathematischer Probleme zu verwenden. Kommen wir zum Punkt.
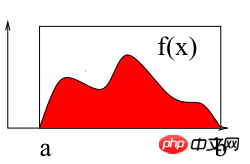
Wie in der obigen Abbildung gezeigt, besteht die Berechnung des Integrals von f(x) im Intervall [ab] darin, die Fläche des roten Bereichs zu ermitteln, der von der eingeschlossen ist Kurve und der X-Achse. Im Folgenden wird die Monte-Carlo-Methode verwendet, um das bestimmte Integral im Intervall [2 3] zu berechnen: ∫(x2+4*x*sin(x))dx
Das Merkmal der Wichtigkeitsstichprobenmethode besteht darin, dass sie nicht aus der Wahrscheinlichkeitsverteilung eines bestimmten Prozesses Stichproben zieht, sondern aus einer modifizierten Wahrscheinlichkeitsverteilung, sodass Ereignisse, die für die Simulationsergebnisse wichtig sind, häufiger auftreten. Dadurch wird die Stichprobeneffizienz verbessert und die Rechenzeit reduziert, die für Ereignisse aufgewendet wird, die für die Simulationsergebnisse unbedeutend sind. Ermitteln Sie beispielsweise das Integral von g(x) im Intervall [a b]. Wenn eine gleichmäßige Abtastung verwendet wird, entspricht die Anzahl der in dem Intervall erzeugten Abtastpunkte, in denen der Funktionswert g(x) relativ klein ist, der Anzahl Wenn die Abtastpunkte in dem Intervall erzeugt werden, in dem der Funktionswert groß ist, ist die Abtasteffizienz offensichtlich nicht hoch. Sie können die Abtastwahrscheinlichkeitsdichtefunktion in f(x) ändern, sodass die Formen von f(x) und g( x) sind ähnlich, wodurch sichergestellt werden kann, dass die Wahrscheinlichkeit des Auftretens von Abtastwerten, die einen großen Beitrag zur Integralberechnung leisten, größer ist als der Abtastwert mit geringem Beitrag, d. h. die Integraloperation kann wie folgt umgeschrieben werden:
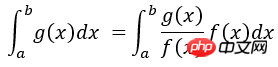
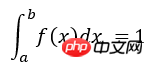
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x**2 + 4*x*np.sin(x)
def intf(x):
return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)
a = 2;
b = 3;
# use N draws
N= 10000
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
# 蒙特卡洛法计算定积分:面积=宽度*平均高度
Imc= (b-a) * np.sum(Y)/ N;
exactval=intf(b)-intf(a)
print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)
# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral
# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.
Imc=np.zeros(1000)
Na = np.linspace(0,1000,1000)
exactval= intf(b)-intf(a)
for N in np.arange(0,1000):
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b
Y =f(X) # CALCULATE THE f(x)
Imc[N]= (b-a) * np.sum(Y)/ N;
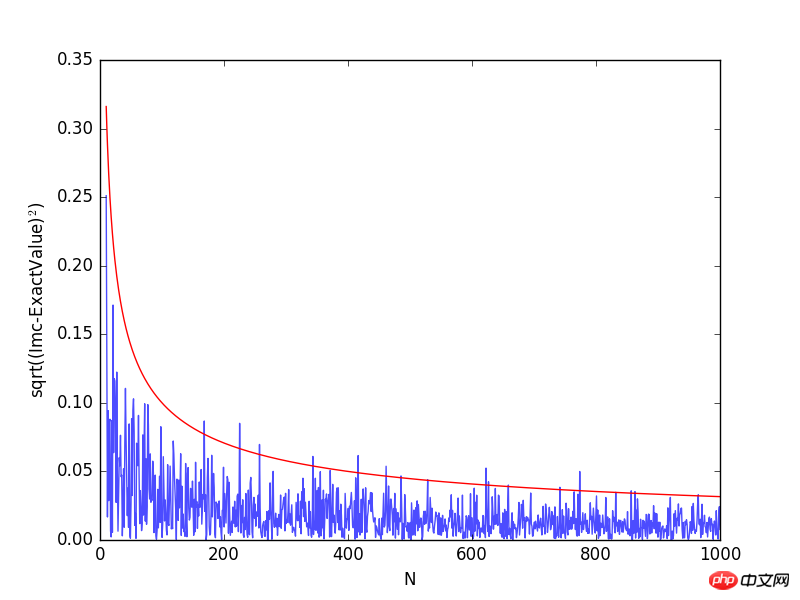
plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)
plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')
plt.xlabel("N")
plt.ylabel("sqrt((Imc-ExactValue)$^2$)")
plt.show()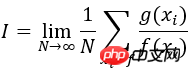
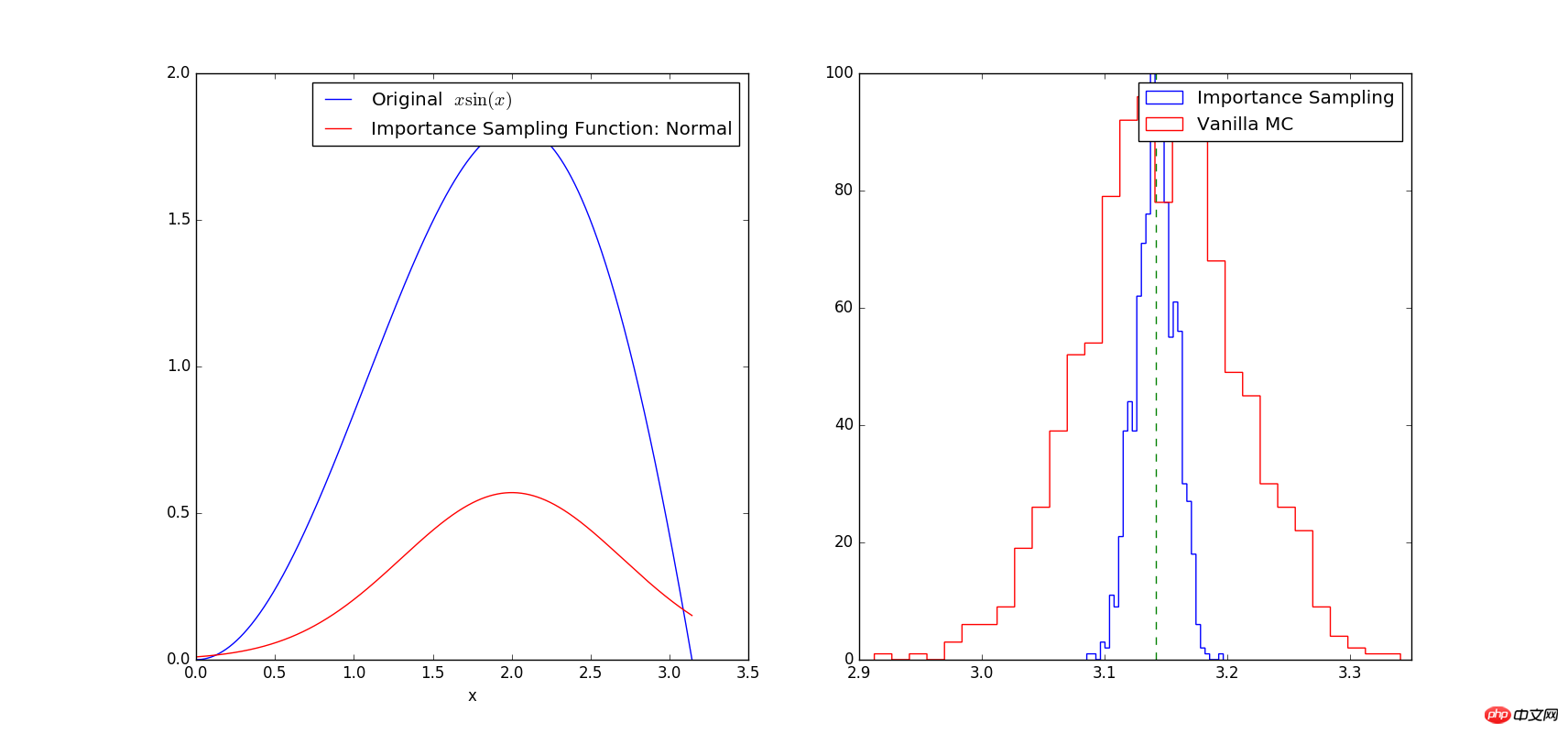
Aus der Abbildung ist ersichtlich, dass die Form der Kurve sin(x)*x der Form der Normalverteilungskurve ähnelt, sodass die Anzahl der Abtastpunkte an der Spitze der Kurve größer ist als die Position auf der Kurve Es gibt mehr Tiefstellen. Das Ergebnis der genauen Berechnung ist pi. Wie aus dem rechten Bild oben hervorgeht, berechnen beide Methoden das bestimmte Integral 1000 Mal. Die Ergebnisse liegen am weitesten vom genauen Wert entfernt. Je kleiner die Zahl, desto offensichtlicher ist dies im Einklang mit der herkömmlichen. Der Unterschied im Quadrat des Integralwerts, der mit der traditionellen Methode (rotes Histogramm) berechnet wird, ist jedoch deutlich größer als bei der wichtigen Stichprobenmethode (blaues Histogramm). Daher kann die Verwendung der Wichtigkeitsstichprobenmethode zur Berechnung die Varianz verringern und die Genauigkeit verbessern. Darüber hinaus ist zu beachten, dass die Wahl der Funktion f(x) die Genauigkeit der Berechnungsergebnisse beeinflusst. Wenn sich die von uns gewählte Funktion f(x) stark von g(x) unterscheidet, wird die Varianz der Berechnungsergebnisse variieren auch erhöhen.
Verwandte Empfehlungen:
So verwenden Sie NotImplementedError in Python programming_python
Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung der Python-Programmierung zur Berechnung bestimmter Integrale mithilfe der Monte-Carlo-Methode. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




