
Dieser Artikel stellt hauptsächlich die Implementierung des neuronalen Netzwerkalgorithmus (BP) und seine einfache Anwendung im Detail vor. Er hat einen bestimmten Referenzwert.
Die Beispiele in diesem Artikel werden mit anderen geteilt Der spezifische Code zum Implementieren neuronaler Netzwerkalgorithmen und -anwendungen in Python wird als Referenz bereitgestellt:
Verwenden Sie zunächst Python, um einen einfachen neuronalen Netzwerkalgorithmus zu implementieren:
import numpy as np
# 定义tanh函数
def tanh(x):
return np.tanh(x)
# tanh函数的导数
def tan_deriv(x):
return 1.0 - np.tanh(x) * np.tan(x)
# sigmoid函数
def logistic(x):
return 1 / (1 + np.exp(-x))
# sigmoid函数的导数
def logistic_derivative(x):
return logistic(x) * (1 - logistic(x))
class NeuralNetwork:
def __init__(self, layers, activation='tanh'):
"""
神经网络算法构造函数
:param layers: 神经元层数
:param activation: 使用的函数(默认tanh函数)
:return:none
"""
if activation == 'logistic':
self.activation = logistic
self.activation_deriv = logistic_derivative
elif activation == 'tanh':
self.activation = tanh
self.activation_deriv = tan_deriv
# 权重列表
self.weights = []
# 初始化权重(随机)
for i in range(1, len(layers) - 1):
self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25)
self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25)
def fit(self, X, y, learning_rate=0.2, epochs=10000):
"""
训练神经网络
:param X: 数据集(通常是二维)
:param y: 分类标记
:param learning_rate: 学习率(默认0.2)
:param epochs: 训练次数(最大循环次数,默认10000)
:return: none
"""
# 确保数据集是二维的
X = np.atleast_2d(X)
temp = np.ones([X.shape[0], X.shape[1] + 1])
temp[:, 0: -1] = X
X = temp
y = np.array(y)
for k in range(epochs):
# 随机抽取X的一行
i = np.random.randint(X.shape[0])
# 用随机抽取的这一组数据对神经网络更新
a = [X[i]]
# 正向更新
for l in range(len(self.weights)):
a.append(self.activation(np.dot(a[l], self.weights[l])))
error = y[i] - a[-1]
deltas = [error * self.activation_deriv(a[-1])]
# 反向更新
for l in range(len(a) - 2, 0, -1):
deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]))
deltas.reverse()
for i in range(len(self.weights)):
layer = np.atleast_2d(a[i])
delta = np.atleast_2d(deltas[i])
self.weights[i] += learning_rate * layer.T.dot(delta)
def predict(self, x):
x = np.array(x)
temp = np.ones(x.shape[0] + 1)
temp[0:-1] = x
a = temp
for l in range(0, len(self.weights)):
a = self.activation(np.dot(a, self.weights[l]))
return a
Verwenden Sie Ihren eigenen definierten neuronalen Netzwerkalgorithmus, um einige einfache Funktionen zu implementieren:
Kleiner Fall:
X: Y
0 0 0
0 1 1
1 0 1
1 1 0
from NN.NeuralNetwork import NeuralNetwork import numpy as np nn = NeuralNetwork([2, 2, 1], 'tanh') temp = [[0, 0], [0, 1], [1, 0], [1, 1]] X = np.array(temp) y = np.array([0, 1, 1, 0]) nn.fit(X, y) for i in temp: print(i, nn.predict(i))
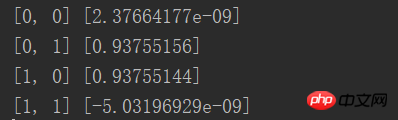
Die Ergebnisse sind grundsätzlich Mechanismus, unbegrenzt nahe 0 oder unendlich nahe 1
Zweites Beispiel: Zahlen in Bildern identifizieren
Daten importieren:
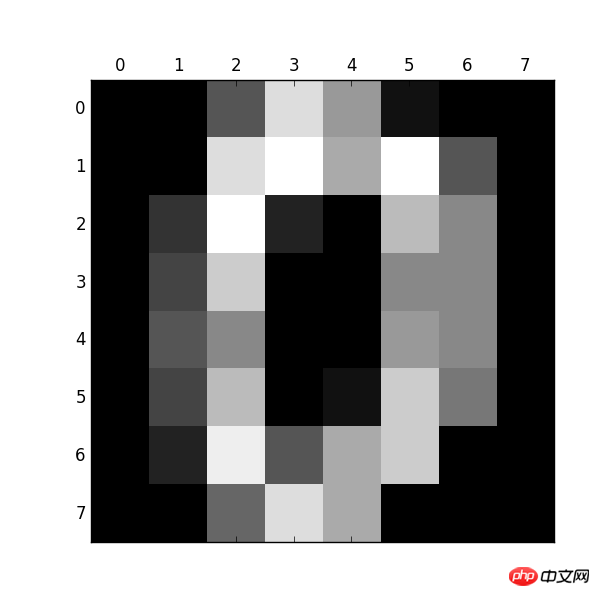
from sklearn.datasets import load_digits import pylab as pl digits = load_digits() print(digits.data.shape) pl.gray() pl.matshow(digits.images[0]) pl.show()
Beobachten Sie: Größe: (1797, 64)
Nummer 0
Der nächste Code dient zur Identifizierung :
import numpy as np
from sklearn.datasets import load_digits
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.preprocessing import LabelBinarizer
from NN.NeuralNetwork import NeuralNetwork
from sklearn.cross_validation import train_test_split
# 加载数据集
digits = load_digits()
X = digits.data
y = digits.target
# 处理数据,使得数据处于0,1之间,满足神经网络算法的要求
X -= X.min()
X /= X.max()
# 层数:
# 输出层10个数字
# 输入层64因为图片是8*8的,64像素
# 隐藏层假设100
nn = NeuralNetwork([64, 100, 10], 'logistic')
# 分隔训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y)
# 转化成sklearn需要的二维数据类型
labels_train = LabelBinarizer().fit_transform(y_train)
labels_test = LabelBinarizer().fit_transform(y_test)
print("start fitting")
# 训练3000次
nn.fit(X_train, labels_train, epochs=3000)
predictions = []
for i in range(X_test.shape[0]):
o = nn.predict(X_test[i])
# np.argmax:第几个数对应最大概率值
predictions.append(np.argmax(o))
# 打印预测相关信息
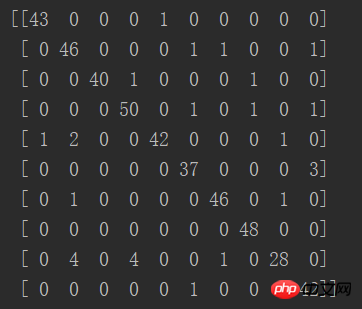
print(confusion_matrix(y_test, predictions))
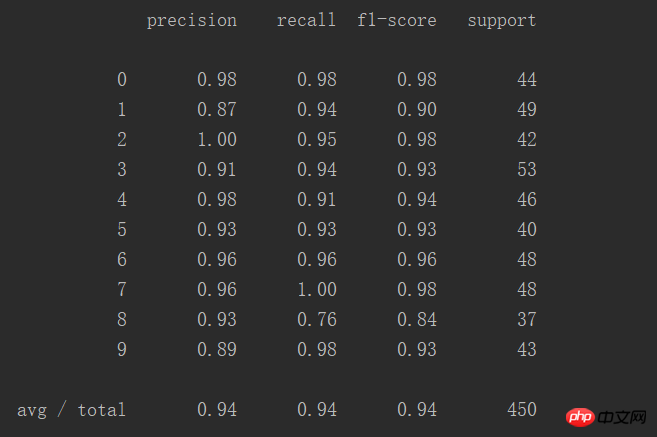
print(classification_report(y_test, predictions))Ergebnis:
Die Diagonale der Matrix stellt die Anzahl der richtigen Vorhersagen dar, und es wird festgestellt, dass die richtige Rate vorliegt ist viele
Diese Tabelle zeigt die Vorhersagegenauigkeit intuitiver:
Insgesamt 450 Fälle, die Erfolgsquote beträgt 94 %
Verwandte Empfehlungen:
KNN-Algorithmus-Python-Implementierung und einfache Zahlenerkennungsmethode
Das obige ist der detaillierte Inhalt vonImplementierung und Anwendung des Python-Algorithmus für neuronale Netze (BP).. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




