
Python的拿手好戏是解决数据分析和可视化问题,本篇文章给大家分享的是python代码画出爱心曲线的操作详解,内容挺不错的,希望可以帮助到有需要的朋友。
先不急着画爱心线,来看如何画函数曲线。
例如,画出指定区间的一个多项式函数:
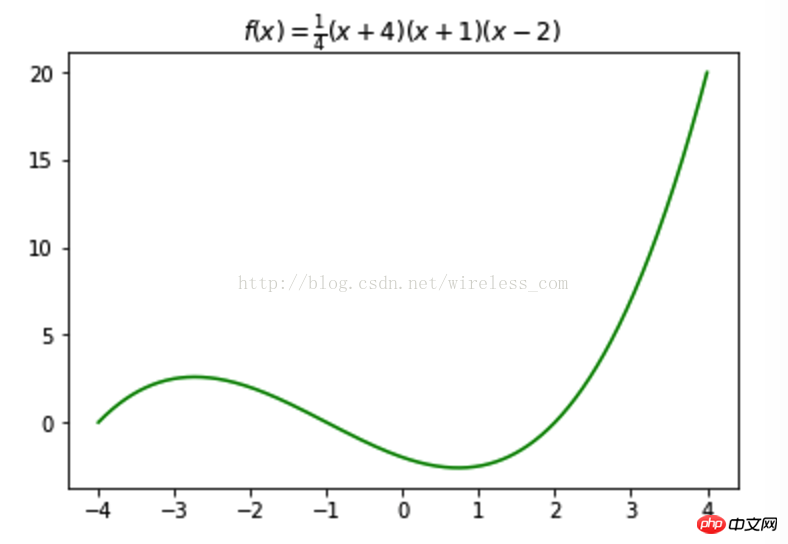
Python 代码如下:
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-4, 4, 1024)
Y = .25 * (X + 4.) * (X + 1.) * (X - 2.)
plt.title('$f(x)=\\frac{1}{4}(x+4)(x+1)(x-2)$')
plt.plot(X, Y, c = 'g')
plt.show()通过numpy的linspace方法来确定横坐标x的取值范围,列出方程,然后调用matplotlib的pyplot画出函数曲线即可。numpy 是一个用python实现的科学计算包,包括一个强大的N维数组对象Array和成熟的函数库,有用于整合C/C++和Fortran代码的工具包,提供了实用的线性代数、傅里叶变换和随机数生成函数等工具,可以理解成Matlab。
记得中学的时候,我问老师三角函数到底有啥用?(无知者无畏)老师反问我,“如果给了你一块洋铁,怎样才能剪出煤炉烟囱的拐弯呢?”,现在仍然记得老师的这个例子,哪些看似抽象的数学公式,实际上是自己不知道她们的应用场景而已。

Python代码如下:
import numpy as np import matplotlib.pyplot as plt X = np.linspace(0, 2 * np.pi, 100) YSinValues = np.sin(X) YCosValues = np.cos(X) plt.plot(X, YSinValues) plt.plot(X, YCosValues) plt.show()
Matplotlib 是一个 Python 的 2D绘图库,甚至可以生成出版质量级别的图形。
对于那些正态分布而言,Python 画起来也就相当简单了:
import numpy as np import matplotlib.pyplot as plt def pdf(X, mu, sigma): a = 1. / (sigma * np.sqrt(2. * np.pi)) b = -1. / (2. * sigma ** 2) return a * np.exp(b * (X - mu) ** 2) X = np.linspace(-6, 6, 1000) for i in range(3): samples = np.random.standard_normal(10) mu, sigma = np.mean(samples), np.std(samples) plt.plot(X, pdf(X, mu, sigma), color = '.66') plt.plot(X, pdf(X, 0., 1.), color = 'b') plt.show()
为了不显得单调,这里多画了几条曲线。只要算出方差和均值,从excel中读出哪些数值就可以拟合正态分布了。

回归到主题,关于爱心线,有这样一个凄美的爱情故事。
迩来流浪于吴越,一片闲云空皎洁。
Vor mehr als 300 Jahren lebte der heruntergekommene Descartes auf den Straßen Stockholms ein Bettelleben und hatte seinen gesamten Besitz, darunter zerschlissene Kleidung und ein paar Mathematikbücher, bei sich. Der distanzierte Descartes bat die Passanten nicht um Almosen, sondern senkte schweigend den Kopf und schrieb und zeichnete auf dem Papier, versunken in seine mathematische Welt. An einem ruhigen Nachmittag saß Descartes wie immer im Sonnenschein auf der Straße und studierte mathematische Probleme. Die vorbeiziehenden Menschenmengen und der Lärm von Kutschen und Pferden konnten ihn nicht stören.
Es gibt einen wunderschönen Menschen, anmutig und elegant. Wir treffen uns zufällig, und wir treffen uns zufällig.
„Was machst du?“ Als Descartes den Kopf drehte, sah er ein junges und schönes Gesicht, ein Paar klarer Augen wie azurblaues Seewasser, so bezaubernd und bezaubernd. Sie war die kleine Prinzessin von Schweden . Christine, die Lieblingstochter des Königs. Sie kniete nieder, nahm Descartes' Mathematikbuch und das Rubbelpapier und begann mit ihm zu reden. Während des Gesprächs stellte er fest, dass dieses kleine Mädchen schnell dachte und ein starkes Interesse an Mathematik hatte.
Einige Tage später erhielt Descartes unerwartet die Nachricht, dass der König ihn als Mathematiklehrer der kleinen Prinzessin eingestellt hatte. Voller Zweifel folgte Descartes den Wachen zum Palast. Aus der Ferne hörte er ein silbernes, glockenartiges Gelächter. Er sah das Mädchen, das er an diesem Tag auf der Straße traf, und wurde fortan der Mathematiklehrer der Prinzessin.
Ich weiß nicht, wo die Liebe begann, aber sie geht tiefer
Die Mathematik der Prinzessin verbesserte sich unter Descartes' Sorgfalt sprunghaft Führung, und auch die Beziehung zwischen ihnen begann sich zu entwickeln. Descartes machte sie mit dem rechteckigen Koordinatensystem bekannt, das die Kombination von Algebra und Geometrie ermöglichte, dem Prototyp der analytischen Geometrie, den Descartes später schaffen sollte. Unter der Anleitung von Descartes betrat Christine die wunderbare Welt der Koordinaten und entwickelte eine Faszination für Kurven. Da sie jeden Tag unzertrennlich waren, verliebten sie sich auch ineinander.
In Schweden, einem romantischen Land, keimte still und leise eine reine und schöne Liebe.
Während ich darüber nachdenke, sehe ich Tausende Meilen Nebel und die Dämmerung versinkt am Himmel.
Als die Nachricht von ihrer Liebesaffäre die Ohren des Königs erreichte, war der König wütend und befahl die Hinrichtung von Descartes. Auf Christines Bitte hin verbannte ihn der König zurück in sein Land und die Prinzessin wurde im Palast unter Hausarrest gestellt.
Zu dieser Zeit breitete sich der Schwarze Tod auf dem europäischen Kontinent aus. Kurz nachdem Descartes nach Frankreich zurückgekehrt war, wurde er schwer krank. Was er in den Tagen, in denen sein Leben ablief, Tag und Nacht vermisste, war das warme, lächelnde Gesicht, das er zufällig auf der Straße traf. Er schrieb ihr jeden Tag und freute sich auf ihre Antwort. Diese Briefe wurden jedoch vom König abgefangen und die Prinzessin erhielt nie eine Nachricht von ihm.
Wenn Sie wissen wollen, was in Ihrem Herzen vorgeht, lesen Sie das Buch in Ihrem Bauch
在笛卡尔给克里斯汀寄出第十三封信后,他永远地离开了这个世界。此时,被软禁在宫中的小公主依然徘徊在皇宫的走廊里,思念着远方的情人。
这最后一封信上没有写一句话,只有一个方程:r=a(1-sinθ)。
国王以为这个方程里隐藏着两个人的秘密,便把全城的数学家召集到皇宫,但是没有人能解开这个函数式。他不忍看着心爱的女儿每天闷闷不乐,便把这封信给了她。拿到信的克里斯汀欣喜若狂,她立即明白了恋人的意图,找来纸和笔,把图形画了出来,一颗心形图案出现在眼前,克里斯汀泪流满面,这条曲线就是著名的“心形线”。
国王去世后,克里斯汀继承王位,便立刻派人去法国寻找心上人的下落,收到的却是笛卡尔去世的消息,留下了一个永远的遗憾…… 这封享誉世界的另类情书,据说至今还保存在欧洲笛卡尔的纪念馆里。
这个故事的出处无从知道,网络上流传着各种各样的版本,甚至在百度百科也有着这个故事。后来,有人考证了真实性,认为这是一个美丽的谎言,但并不妨碍人们对爱心线喜爱。
在直角坐标系中,爱心线的方程的python 表达为:x** 2+ y** 2 + a * x= a * sqrt(x** 2+y** 2) 和 x** 2+ y** 2 - a * x= a * sqrt(x** 2+y** 2)通过x 来求对应的y值很麻烦,就像软件设计中的“万能层”那样,可以采用参数方程来表示:
x=a*(2*cos(t)-cos(2*t)) y=a*(2*sin(t)-sin(2*t))
具体的python代码如下:
import numpy as np import matplotlib.pyplot as plt a = 1 t = np.linspace(0 , 2 * np.pi, 1024) X = a*(2*np.cos(t)-np.cos(2*t)) Y = a*(2*np.sin(t)-np.sin(2*t)) plt.plot(Y, X,color='r') plt.show()
代表爱心的心形线来了:
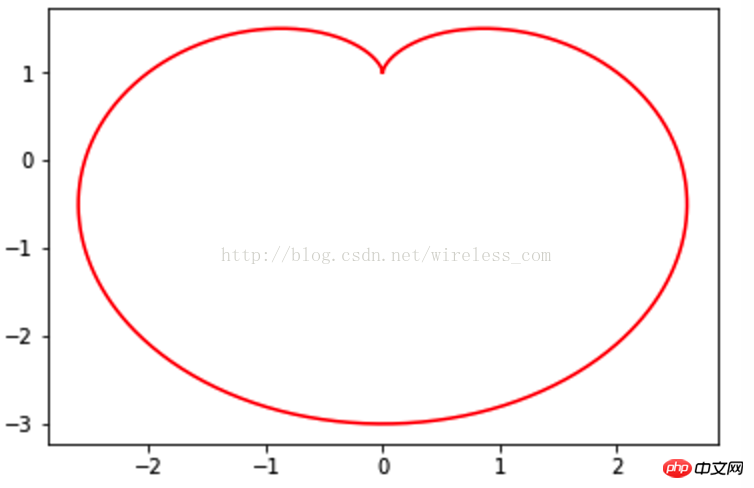
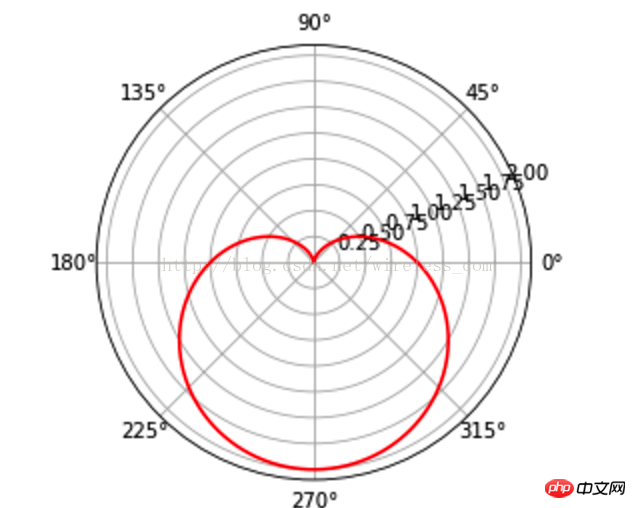
但这不是六行代码呀?也不是r=a(1-sinθ)呀? 的确如此,那是极坐标系,python 的matplotlib同样支持极坐标系的,爱心线的六行pyton代码如下:
import numpy as np import matplotlib.pyplot as plt T = np.linspace(0 , 2 * np.pi, 1024) plt.axes(polar = True) plt.plot(T, 1. - np.sin(T),color="r") plt.show()
这样,得到的就是封面中的图像了:
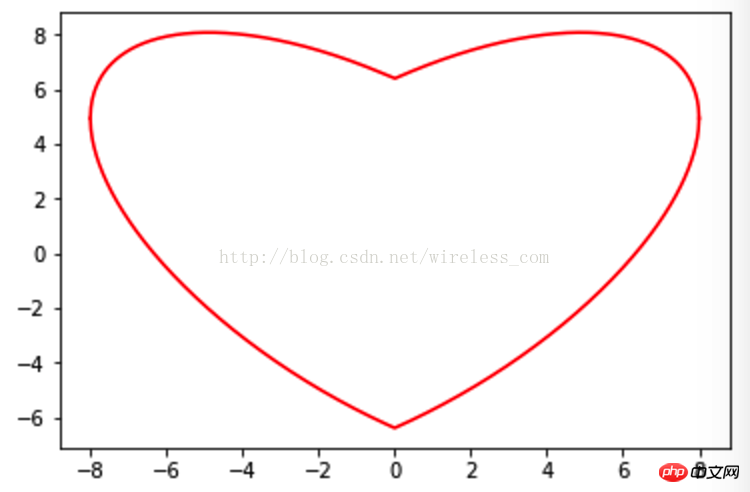
心形线确实是爱心满满,如果融入了忧伤会是怎样呢?
import numpy as np import matplotlib.pyplot as plt x = np.linspace(-8 , 8, 1024) y1 = 0.618*np.abs(x) - 0.8* np.sqrt(64-x**2) y2 = 0.618*np.abs(x) + 0.8* np.sqrt(64-x**2) plt.plot(x, y1, color = 'r') plt.plot(x, y2, color = 'r') plt.show()
这样就得到了另一个爱心线:
Es gibt verschiedene schöne Implementierungen von Liebeslinien im Internet, und sie sind auch voller verschiedener Emotionen, aber für jede davon können sie im Grunde relativ einfach mit Python implementiert werden.
Eigentlich ist das Zeichnen sehr einfach. Was schwierig ist, ist der Ausdruck dieser Kurvengleichungen und der tatsächlichen Anforderungen des Anwendungsszenarios , wie z. B. Spirale.
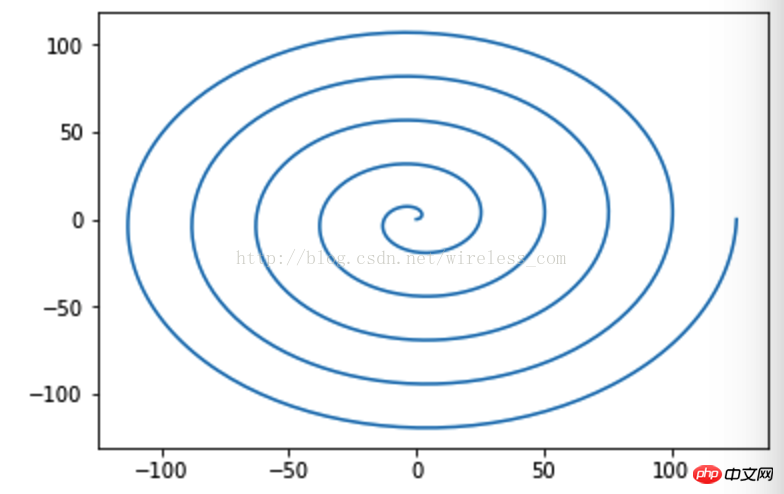
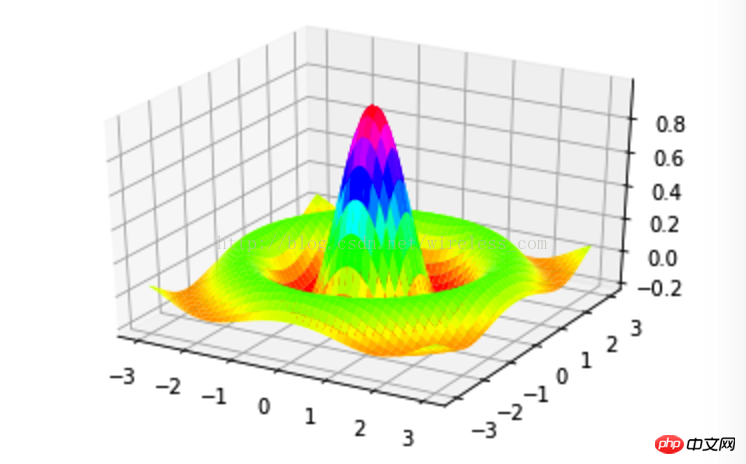
Ferner, Sie können auch verschiedene 3D-Ansichten zeichnen, wie zum Beispiel:
Zusammenfassung:
Als letztes Glied in der Datenanalyse und sogar in der Big-Data-Verarbeitung handelt es sich um die sogenannte Visualisierung von Erkenntnissen, und Python kann es sein soll eines davon sein.
Das obige ist der detaillierte Inhalt vonPython-Code zeichnet eine Liebeskurve. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




