Implementierung des Dijkstra-Algorithmus für den Kürzeste-Pfad-Algorithmus in Java-javaLernprogramm-php.cn

In diesem Artikel wird hauptsächlich der Dijkstra-Algorithmus vorgestellt, der den kürzesten Pfadalgorithmus in Java implementiert. Interessierte können mehr darüber erfahren

Vorwort

Dijkstras Algorithmus ist ein bekannter Kürzestpfad-Algorithmus und ein Single-Start-Vollpfadalgorithmus. Dieser Algorithmus wird als erfolgreiches Beispiel für einen „Greedy-Algorithmus“ bezeichnet. In diesem Artikel wird versucht, diesen großartigen Algorithmus in der beliebtesten Sprache vorzustellen und ihm Java-Implementierungscode zu geben.

1. Wissensvorbereitung:

1. Die Datenstruktur, die das Diagramm darstellt:

Es gibt viele Datenstrukturen zum Speichern von Diagrammen. In diesem Algorithmus verwendet der Autor die Adjazenzmatrix.

Die Adjazenzmatrix-Speichermethode eines Diagramms besteht darin, zwei Arrays zur Darstellung des Diagramms zu verwenden. Ein eindimensionales Array speichert Scheitelpunktinformationen im Diagramm, und ein zweidimensionales Array (Adjazenzmatrix) speichert Kanten- oder Bogeninformationen im Diagramm.

Angenommen, der Graph G hat n Eckpunkte, dann ist die Adjazenzmatrix eine n*n-Quadratmatrix, definiert als:

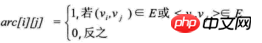
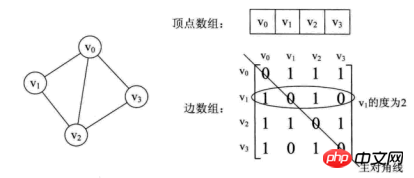
Wie aus dem Obigen ersichtlich ist, ist das Kantenarray eines ungerichteten Graphen eine symmetrische Matrix. Die sogenannte symmetrische Matrix bedeutet, dass die Elemente der Matrix n-ter Ordnung aij = aji erfüllen. Das heißt, die Hauptdiagonale von der oberen linken Ecke zur unteren rechten Ecke der Matrix ist die Achse, und die Elemente in der oberen rechten Ecke und die entsprechenden Elemente in der unteren linken Ecke sind alle gleich.

Anhand dieser Matrix ist es leicht, die Informationen im Bild zu erkennen.

(1) Es ist sehr einfach zu bestimmen, ob zwei beliebige Scheitelpunkte Kanten haben oder keine Kanten.

(2) Den Grad eines bestimmten Scheitelpunkts zu kennen, bedeutet tatsächlich, dass der Scheitelpunkt vi ist der dritte in der Adjazenzmatrix. Die Summe der Elemente in Zeile i oder (i-te Spalte);

(3) Um alle benachbarten Punkte von Scheitelpunkt vi zu finden, muss der i-te gescannt werden Zeilenelemente in der Matrix sind einmal, arc[i][j] ist 1. Benachbarte Punkte

Und gerichtete Graphen achten auf In-Grad und Out-Grad. Der In-Grad des Scheitelpunkts vi ist 1, Das ist genau die Summe der Zahlen in der i-ten Spalte. Der Out-Grad des Scheitelpunkts vi ist 2, was der Summe der Zahlen in der i-ten Zeile entspricht.

Die Definition des gerichteten Graphen ist ebenfalls ähnlich, daher werden keine Details angegeben.

2. Einzelstartpunkt-Vollpfad

Der sogenannte Einzelstartpunkt-Vollpfad bezieht sich auf den kürzesten Pfad, der von einem Startpunkt zu allen Knoten in einem Diagramm beginnt .

3. Grundkenntnisse der Graphentheorie (Leser müssen relevante Informationen selbst finden)

4. Komplementäre Entspannungsbedingungen

Angenommen, der Skalar d1, d2,....,dN erfüllt

dj<=di + aij, (i,j) gehört zu A,

und P ist mit i1 as der Startpunkt und ik als Endpunktpfad, wenn

dj = di + aij,

für alle Kanten (i, j) von P gilt, dann ist P der kürzeste Weg von i1 zu ik. Darunter werden die komplementären Relaxationsbedingungen des Kürzeste-Wege-Problems genannt, die die beiden obigen Gleichungen erfüllen.

2. Algorithmusidee

1. Sei G = (V, E) ein gewichteter ungerichteter Graph. Wenn es in G zwei benachbarte Knoten gibt, i und j. aij (hier und später als Index ausgedrückt, bitte beachten) ist das Gewicht vom Knoten i zum Knoten j, was in diesem Algorithmus als Abstand verstanden werden kann. Jeder Knoten hat einen Wert di (Knotenbezeichnung), der seinen Abstand vom Startpunkt zu einem bestimmten Pfad dorthin angibt.

2. Der Algorithmus verfügt zunächst über ein Array V, in dem eine Liste nicht besuchter Knoten gespeichert wird, die wir vorübergehend als Kandidatenliste bezeichnen. Wählen Sie Knoten 1 als Startknoten. Zu Beginn gilt d1=0 für Knoten 1, di=unendlich für andere Knoten und V für alle Knoten.
Starten Sie nach der Initialisierung der Bedingungen den iterativen Algorithmus und stoppen Sie, wenn V die leere Menge ist. Die spezifischen Iterationsschritte lauten wie folgt:

Entfernen Sie den Knoten di mit dem kleinsten d-Wert aus der Kandidatenliste. (In diesem Beispiel verwendet die Datenstruktur von V eine Prioritätswarteschlange, um das Entfernen des Mindestwerts aus der Warteschlange zu implementieren. Es ist am besten, Fibonacci-Paare zu verwenden, die in früheren Artikeln eingeführt wurden, und die Leistung wird erheblich verbessert.) Für jede Kante, die von diesem Knoten ausgeht, mit Ausnahme des Knotens, an dem V entfernt wird, gehört (i, j) zu A. Wenn dj > di + aij (Verletzung der Relaxationsbedingung), sei

dj = di + aij , (wenn j von V entfernt wurde, bedeutet dies, dass sein Mindestabstand berechnet wurde und nicht an dieser Berechnung teilnimmt)

Es ist ersichtlich, dass im Berechnungsprojekt des Algorithmus das d Der Wert des Knotens lautet: Das spezifische Algorithmusdiagramm für monoton nicht zunehmendes

lautet wie folgt:

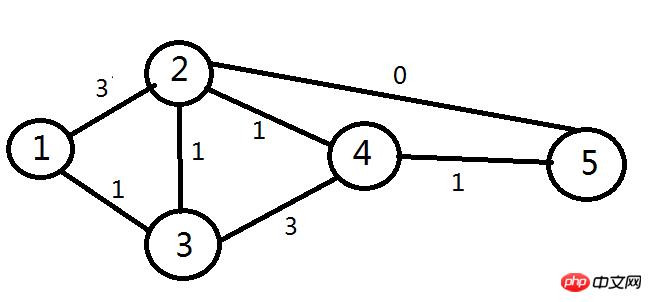
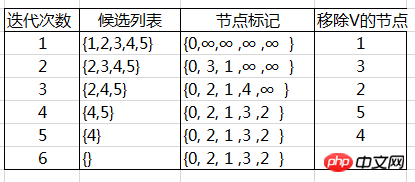
3. Java-Code-Implementierung

public class Vertex implements Comparable<Vertex>{

  /**
   * 节点名称(A,B,C,D)
   */
  private String name;
  
  /**
   * 最短路径长度
   */
  private int path;
  
  /**
   * 节点是否已经出列(是否已经处理完毕)
   */
  private boolean isMarked;
  
  public Vertex(String name){
    this.name = name;
    this.path = Integer.MAX_VALUE; //初始设置为无穷大
    this.setMarked(false);
  }
  
  public Vertex(String name, int path){
    this.name = name;
    this.path = path;
    this.setMarked(false);
  }
  
  @Override
  public int compareTo(Vertex o) {
    return o.path > path?-1:1;
  }
}

Nach dem Login kopieren

public class Graph {

  /*
   * 顶点
   */
  private List<Vertex> vertexs;

  /*
   * 边
   */
  private int[][] edges;

  /*
   * 没有访问的顶点
   */
  private Queue<Vertex> unVisited;

  public Graph(List<Vertex> vertexs, int[][] edges) {
    this.vertexs = vertexs;
    this.edges = edges;
    initUnVisited();
  }
  
  /*
   * 搜索各顶点最短路径
   */
  public void search(){
    while(!unVisited.isEmpty()){
      Vertex vertex = unVisited.element();
      //顶点已经计算出最短路径，设置为"已访问"
     　　vertex.setMarked(true);  
      //获取所有"未访问"的邻居
      　　List<Vertex> neighbors = getNeighbors(vertex);  
      //更新邻居的最短路径
      updatesDistance(vertex, neighbors);    
      pop();
    }
    System.out.println("search over");
  }
  
  /*
   * 更新所有邻居的最短路径
   */
  private void updatesDistance(Vertex vertex, List<Vertex> neighbors){
    for(Vertex neighbor: neighbors){
      updateDistance(vertex, neighbor);
    }
  }
  
  /*
   * 更新邻居的最短路径
   */
  private void updateDistance(Vertex vertex, Vertex neighbor){
    int distance = getDistance(vertex, neighbor) + vertex.getPath();
    if(distance < neighbor.getPath()){
      neighbor.setPath(distance);
    }
  }

  /*
   * 初始化未访问顶点集合
   */
  private void initUnVisited() {
    unVisited = new PriorityQueue<Vertex>();
    for (Vertex v : vertexs) {
      unVisited.add(v);
    }
  }

  /*
   * 从未访问顶点集合中删除已找到最短路径的节点
   */
  private void pop() {
    unVisited.poll();
  }

  /*
   * 获取顶点到目标顶点的距离
   */
  private int getDistance(Vertex source, Vertex destination) {
    int sourceIndex = vertexs.indexOf(source);
    int destIndex = vertexs.indexOf(destination);
    return edges[sourceIndex][destIndex];
  }

  /*
   * 获取顶点所有(未访问的)邻居
   */
  private List<Vertex> getNeighbors(Vertex v) {
    List<Vertex> neighbors = new ArrayList<Vertex>();
    int position = vertexs.indexOf(v);
    Vertex neighbor = null;
    int distance;
    for (int i = 0; i < vertexs.size(); i++) {
      if (i == position) {
        //顶点本身，跳过
        continue;
      }
      distance = edges[position][i];  //到所有顶点的距离
      if (distance < Integer.MAX_VALUE) {
        //是邻居(有路径可达)
        neighbor = getVertex(i);
        if (!neighbor.isMarked()) {
          //如果邻居没有访问过，则加入list;
          neighbors.add(neighbor);
        }
      }
    }
    return neighbors;
  }

  /*
   * 根据顶点位置获取顶点
   */
  private Vertex getVertex(int index) {
    return vertexs.get(index);
  }

  /*
   * 打印图
   */
  public void printGraph() {
    int verNums = vertexs.size();
    for (int row = 0; row < verNums; row++) {
      for (int col = 0; col < verNums; col++) {
        if(Integer.MAX_VALUE == edges[row][col]){
          System.out.print("X");
          System.out.print(" ");
          continue;
        }
        System.out.print(edges[row][col]);
        System.out.print(" ");
      }
      System.out.println();
    }
  }
}

Nach dem Login kopieren

public class Test {

  public static void main(String[] args){
    List<Vertex> vertexs = new ArrayList<Vertex>();
    Vertex a = new Vertex("A", 0);
    Vertex b = new Vertex("B");
    Vertex c = new Vertex("C");
    Vertex d = new Vertex("D");
    Vertex e = new Vertex("E");
    Vertex f = new Vertex("F");
    vertexs.add(a);
    vertexs.add(b);
    vertexs.add(c);
    vertexs.add(d);
    vertexs.add(e);
    vertexs.add(f);
    int[][] edges = {
        {Integer.MAX_VALUE,6,3,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {6,Integer.MAX_VALUE,2,5,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {3,2,Integer.MAX_VALUE,3,4,Integer.MAX_VALUE},
        {Integer.MAX_VALUE,5,3,Integer.MAX_VALUE,5,3},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,4,5,Integer.MAX_VALUE,5},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,3,5,Integer.MAX_VALUE}
    
    };
    Graph graph = new Graph(vertexs, edges);
    graph.printGraph();
    graph.search();
  }
  
}

Nach dem Login kopieren

Das obige ist der detaillierte Inhalt vonImplementierung des Dijkstra-Algorithmus für den Kürzeste-Pfad-Algorithmus in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!