So implementieren Sie einen binären Heap in Python-Python-Tutorial-php.cn

Binärer Heap ist eine besondere Art von Heap. Binärer Heap ist ein vollständiger Binärbaum (Binärbaum) oder ein annähernd vollständiger Binärbaum (Binärbaum). Es gibt zwei Arten von binären Heaps: Max-Heap und Min-Heap. Max. Heap: Der Schlüsselwert des übergeordneten Knotens ist immer größer oder gleich dem Schlüsselwert eines beliebigen untergeordneten Knotens. Min. Heap: Der Schlüsselwert des übergeordneten Knotens ist immer kleiner oder gleich dem Schlüsselwert eines beliebigen untergeordneten Knotens.

Binäre Heap-Implementierung der Prioritätswarteschlange

Im vorherigen Kapitel haben wir die Datenstruktur von „First In, First Out“ (FIFO) kennengelernt: Warteschlange (Queue). Es gibt eine Variante der Warteschlange namens „Prioritätswarteschlange“ (Priority Queue). Der Vorgang zum Entfernen (Dequeue) der Prioritätswarteschlange ist derselbe wie der der Warteschlange und wird vom Kopf der Warteschlange entfernt. Innerhalb der Prioritätswarteschlange wird die Reihenfolge der Elemente jedoch durch „Priorität“ bestimmt: Elemente mit hoher Priorität befinden sich vorne in der Warteschlange, während Elemente mit niedriger Priorität hinten stehen. Auf diese Weise ist der Einreihungsvorgang (Enqueue) der Prioritätswarteschlange komplizierter und die Elemente müssen entsprechend der Priorität so weit wie möglich in die Warteschlange gestellt werden. Im nächsten Abschnitt werden wir feststellen, dass Prioritätswarteschlangen eine nützliche Datenstruktur für Diagrammalgorithmen sind.

Wir denken natürlich darüber nach, Sortieralgorithmen und Warteschlangen zu verwenden, um Prioritätswarteschlangen zu implementieren. Der Zeitaufwand für das Einfügen eines Elements in die Liste beträgt jedoch O(n) und der Zeitaufwand für das Sortieren der Liste beträgt O(nlogn). Wir können andere Methoden verwenden, um die Zeitkomplexität zu reduzieren. Eine klassische Möglichkeit, eine Prioritätswarteschlange zu implementieren, ist die Verwendung eines binären Heaps (Binary Heap). Der binäre Heap kann die Komplexität sowohl des Einreihens als auch des Entfernens der Prioritätswarteschlange auf O(logn) halten.

Das Interessante am binären Heap ist, dass seine logische Struktur einem Binärbaum ähnelt, jedoch mit nicht verschachtelten Listen implementiert wird. Es gibt zwei Arten von binären Heaps: Derjenige mit dem kleinsten Schlüsselwert, der immer an der Spitze der Warteschlange steht, wird als „Minimalheap (min heap)“ bezeichnet; umgekehrt wird derjenige mit dem größten Schlüsselwert immer an der Spitze der Warteschlange platziert der Warteschlange wird als „maximaler Heap (max heap) )“ bezeichnet. In diesem Abschnitt verwenden wir Min-Heap.

Operationen des binären Heaps

Die Grundoperationen des binären Heaps sind wie folgt definiert:

BinaryHeap(): Erstellen ein leeres binäres Heap-Objekt
insert(k): Neue Elemente zum Heap hinzufügen
findMin(): Das kleinste Element im Heap zurückgeben Element, das Mindestelement bleibt im Heap
delMin(): Gibt das Mindestelement im Heap zurück und entfernt es gleichzeitig vom Heap
isEmpty(): Gibt zurück, ob der Heap leer ist
size(): Gibt die Anzahl der Knoten im Heap zurück
buildHeap(list) : Aus einem enthaltenden Erstellen Sie einen neuen Heap aus der Liste der Knoten

Der unten gezeigte Code ist ein Beispiel für einen binären Heap. Sie können sehen, dass unabhängig von der Reihenfolge, in der wir Elemente zum Heap hinzufügen, jedes Mal das kleinste Element entfernt wird. Wir werden diesen Prozess als nächstes implementieren.

from pythonds.trees.binheap import BinHeap

bh = BinHeap()
bh.insert(5)
bh.insert(7)
bh.insert(3)
bh.insert(11)

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

Nach dem Login kopieren

Um den Heap besser zu implementieren, verwenden wir einen Binärbaum. Wir müssen immer das „Gleichgewicht“ des Binärbaums aufrechterhalten und die Operation immer auf der logarithmischen Skala halten. Ein ausgeglichener Binärbaum hat die gleiche Anzahl untergeordneter Knoten im linken und rechten Teilbaum des Wurzelknotens. Bei der Implementierung des Heaps verwenden wir die Struktur eines „vollständigen Binärbaums“, um ungefähr ein „Gleichgewicht“ zu erreichen. Ein vollständiger Binärbaum bedeutet, dass jeder interne Knotenbaum seinen Maximalwert erreicht, mit der Ausnahme, dass auf der letzten Ebene nur mehrere Knoten auf der rechten Seite fehlen können. Abbildung 1 zeigt einen vollständigen Binärbaum.

So implementieren Sie einen binären Heap in Python

Abbildung 1: Vollständiger Binärbaum

Interessanterweise können wir mit einer einzigen Liste einen vollständigen Baum erreichen. Wir müssen keine Knoten, Referenzen oder verschachtelten Listen verwenden. Denn wenn für einen vollständigen Binärbaum der Index des Knotens in der Liste p ist, dann ist der Index seines linken untergeordneten Knotens 2p und der Index des rechten Knotens ist 2p + 1. Wenn wir den übergeordneten Knoten eines beliebigen Knotens finden möchten, können wir direkt die Ganzzahldivision von Python verwenden. Wenn ein Knoten in der Liste indiziert ist n, dann wird der übergeordnete Knoten indiziert n//2. Abbildung 2 zeigt einen vollständigen Binärbaum und eine Listendarstellung des Baums. Beachten Sie die 2p- und 2p+1-Beziehungen zwischen übergeordneten Knoten und untergeordneten Knoten. Die Listendarstellung eines vollständigen Baums kombiniert die Eigenschaften eines vollständigen Binärbaums und ermöglicht es uns, einen vollständigen Baum mithilfe einfacher mathematischer Methoden effizient zu durchlaufen. Dadurch können wir auch binäre Heaps effizient implementieren.

Eigenschaften der Heap-Reihenfolge

Die Art und Weise, wie wir Elemente im Heap speichern, hängt von der Reihenfolge des Heaps ab. Die sogenannte Heap-Reihenfolge bedeutet, dass für jeden Knoten x im Heap der Schlüsselwert seines übergeordneten Knotens p kleiner oder gleich dem Schlüsselwert von x ist. Abbildung 2 zeigt einen vollständigen Binärbaum mit Heap-geordneten Eigenschaften.

So implementieren Sie einen binären Heap in Python

Abbildung 2: Vollständiger Baum und seine Listendarstellung

Implementierung der binären Heap-Operation

接下来我们来构造二叉堆。因为可以采用一个列表保存堆的数据，构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。Listing 1 所示的是构造二叉堆的 python 代码。注意到二叉堆的heaplist并没有用到，但为了后面代码可以方便地使用整除，我们仍然保留它。

Listing 1

class BinHeap:
  def init(self):
    self.heapList = [0]
    self.currentSize = 0

Nach dem Login kopieren

我们接下来要实现的是insert方法。首先，为了满足“完全二叉树”的性质，新键值应该添加到列表的末尾。然而新键值简单地添加在列表末尾，显然无法满足堆次序。但我们可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小，可以与父节点互换位置。图 3 所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。

So implementieren Sie einen binären Heap in Python

图 3：新节点“上浮”到其正确位置

当我们让一个元素“上浮”时，我们要保证新节点与父节点以及其他兄弟节点之间的堆次序。当然，如果新节点非常小，我们仍然需要将它交换到其他层。事实上，我们需要不断交换，直到到达树的顶端。Listing 2 所示的是“上浮”方法，它把一个新节点“上浮”到其正确位置来满足堆次序。这里很好地体现了我们之前在headlist中没有用到的元素 0 的重要性。这样只需要做简单的整除，将当前节点的下标除以 2，我们就能计算出任何节点的父节点。

在Listing 3 中，我们已经可以写出insert方法的代码。insert里面很大一部分工作是由percUp函数完成的。当树添加新节点时，调用percUp就可以将新节点放到正确的位置上。

Listing 2

def percUp(self,i):
  while i // 2 > 0:
   if self.heapList[i] < self.heapList[i // 2]:
     tmp = self.heapList[i // 2]
     self.heapList[i // 2] = self.heapList[i]
     self.heapList[i] = tmp
   i = i // 2

Nach dem Login kopieren

Listing 3

def insert(self,k):
  self.heapList.append(k)
  self.currentSize = self.currentSize + 1
  self.percUp(self.currentSize)

Nach dem Login kopieren

我们已经写好了insert方法，那再来看看delMin方法。堆次序要求根节点是树中最小的元素，因此很容易找到最小项。比较困难的是移走根节点的元素后如何保持堆结构和堆次序，我们可以分两步走。首先，用最后一个节点来代替根节点。移走最后一个节点保持了堆结构的性质。这么简单的替换，还是会破坏堆次序。那么第二步，将新节点“下沉”来恢复堆次序。图 4 所示的是一系列交换操作来使新节点“下沉”到正确的位置。

So implementieren Sie einen binären Heap in Python

图 4：替换后的根节点下沉

为了保持堆次序，我们需将新的根节点沿着一条路径“下沉”，直到比两个子节点都小。在选择下沉路径时，如果新根节点比子节点大，那么选择较小的子节点与之交换。Listing 4 所示的是新节点下沉所需的percDown和minChild方法的代码。

Listing 4

def percDown(self,i):
  while (i * 2) <= self.currentSize:
    mc = self.minChild(i)
    if self.heapList[i] > self.heapList[mc]:
      tmp = self.heapList[i]
      self.heapList[i] = self.heapList[mc]
      self.heapList[mc] = tmp
    i = mc

def minChild(self,i):
  if i * 2 + 1 > self.currentSize:
    return i * 2
  else:
    if self.heapList[i*2] < self.heapList[i*2+1]:
      return i * 2
    else:
      return i * 2 + 1

Nach dem Login kopieren

Listing 5 所示的是delMin操作的代码。可以看到比较麻烦的地方由一个辅助函数来处理，即percDown。

Listing 5

def delMin(self):
  retval = self.heapList[1]
  self.heapList[1] = self.heapList[self.currentSize]
  self.currentSize = self.currentSize - 1
  self.heapList.pop()
  self.percDown(1)
  return retval

Nach dem Login kopieren

关于二叉堆的最后一部分便是找到从无序列表生成一个“堆”的方法。我们首先想到的是，将无序列表中的每个元素依次插入到堆中。对于一个排好序的列表，我们可以用二分搜索找到合适的位置，然后在下一个位置插入这个键值到堆中，时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动，为新节点腾出位置，时间复杂度为O(n)。因此用insert方法的总开销是O(nlogn)。其实我们能直接将整个列表生成堆，将总开销控制在O(n)。Listing 6 所示的是生成堆的操作。

Listing 6

def buildHeap(self,alist):
  i = len(alist) // 2
  self.currentSize = len(alist)
  self.heapList = [0] + alist[:]
  while (i > 0):
    self.percDown(i)
    i = i - 1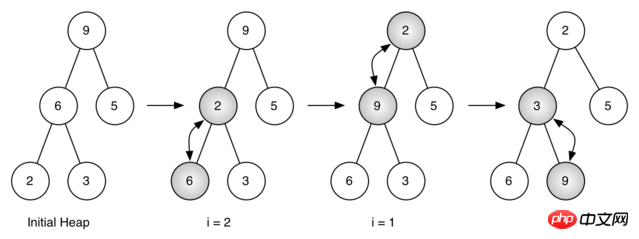

Nach dem Login kopieren

So implementieren Sie einen binären Heap in Python

图 5：将列表[ 9, 6, 5, 2, 3]生成一个二叉堆

图 5 所示的是利用buildHeap方法将最开始的树[ 9, 6, 5, 2, 3]中的节点移动到正确的位置时所做的交换操作。尽管我们从树中间开始，然后回溯到根节点，但percDown方法保证了最大子节点总是“下沉”。因为堆是完全二叉树，任何在中间的节点都是叶节点，因此没有子节点。注意，当i=1时，我们从根节点开始下沉，这就需要进行大量的交换操作。可以看到，图 5 最右边的两颗树，首先 9 从根节点的位置移走，移到下一层级之后，percDown进一步检查它此时的子节点，保证它下降到不能再下降为止，即下降到正确的位置。然后进行第二次交换，9 和 3 的交换。由于 9 已经移到了树最底层的层级，便无法进一步交换了。比较一下列表表示法和图 5 所示的树表示法进行的一系列交换还是很有帮助的。

i = 2 [0, 9, 5, 6, 2, 3]
i = 1 [0, 9, 2, 6, 5, 3]
i = 0 [0, 2, 3, 6, 5, 9]

Nach dem Login kopieren

下列所示的代码是完全二叉堆的实现。

def insert(self,k):
   self.heapList.append(k)
   self.currentSize = self.currentSize + 1
   self.percUp(self.currentSize)

  def percDown(self,i):
   while (i * 2) <= self.currentSize:
     mc = self.minChild(i)
     if self.heapList[i] > self.heapList[mc]:
       tmp = self.heapList[i]
       self.heapList[i] = self.heapList[mc]
       self.heapList[mc] = tmp
     i = mc

  def minChild(self,i):
   if i * 2 + 1 > self.currentSize:
     return i * 2
   else:
     if self.heapList[i*2] < self.heapList[i*2+1]:
       return i * 2
     else:
       return i * 2 + 1

  def delMin(self):
   retval = self.heapList[1]
   self.heapList[1] = self.heapList[self.currentSize]
   self.currentSize = self.currentSize - 1

Nach dem Login kopieren

能在O(n)的开销下能生成二叉堆看起来有点不可思议，其证明超出了本书的范围。但是，要理解用O(n)的开销能生成堆的关键是因为logn因子基于树的高度。而对于buildHeap里的许多操作，树的高度比logn要小。

Das obige ist der detaillierte Inhalt vonSo implementieren Sie einen binären Heap in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!