Detaillierte Erläuterung der JavaScript-Baumstruktur

Jeder muss mit der Datenstruktur „Baum“ vertraut sein. Heute werden wir den Binärbaum und den Baum in der Datenstruktur überprüfen und sie mit JavaScript implementieren.

ps: Die Baumstruktur spiegelt sich an vielen Stellen im Front-End deutlich wider, z. B. im virtuellen DOM von Vue und beim Sprudeln usw.

Binärbaum

--Konzept--

Binärbaum ist eine Baumstruktur, die dadurch gekennzeichnet ist, dass jeder Knoten höchstens zwei Teilbäume hat (d. h. es gibt Nein Es gibt Knoten mit einem Grad größer als 2. Die Teilbäume des Binärbaums können in linke und rechte Teilbäume unterteilt werden, und ihre Reihenfolge kann nicht beliebig umgekehrt werden.

lautet wie folgt, was ein Binärbaum ist (Hinweis: Die folgenden Beispiele für Binärbäume basieren alle auf diesem Binärbaum):

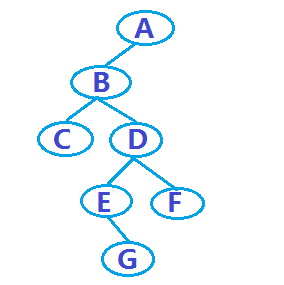
Und, Beim Durchlaufen des Binärbaums (Traversing Binary Tree) gibt es drei häufig verwendete Methoden:

1), Vorbestellungsdurchlauf des Binärbaums (links und rechts von der Wurzel)

Wenn der Binärbaum leer ist, erfolgt keine Operation.

– Den linken Teilbaum der Reihe nach durchlaufen.

– Den rechten Teilbaum durchqueren in Ordnung.

Für den Binärbaum im obigen Beispiel lautet das Durchlaufergebnis beispielsweise wie folgt:

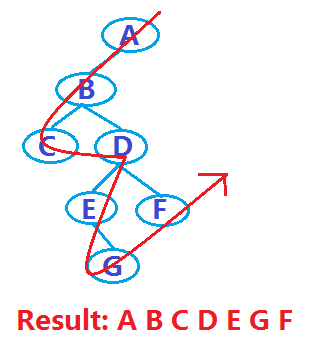2), Durchlauf der Binärdatei in der richtigen Reihenfolge Baum (linke Wurzel rechts)

Wenn der Binärbaum leer ist, sonst keine Operation;

– Durchqueren des linken Teilbaums in der richtigen Reihenfolge

– Besuchen Sie den Wurzelknoten ;

– Durchlauf in der richtigen Reihenfolge Rechter Teilbaum.

Für den Binärbaum im obigen Beispiel lautet das Durchlaufergebnis beispielsweise wie folgt:

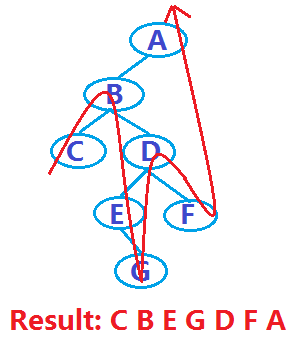3), Durchlauf der Binärdatei nach der Bestellung Baum (linke und rechte Wurzeln)

Wenn der Binärbaum leer ist, sonst

– den linken Teilbaum in der Nachfolge durchqueren;

– den rechten Teilbaum durchqueren Teilbaum in der Nachbestellung;

--besuchen Sie den Wurzelknoten.

Für den Binärbaum im obigen Beispiel lautet das Durchlaufergebnis beispielsweise wie folgt:

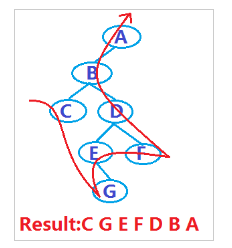Okay, jetzt verstehen wir den Binärbaum und Wie man es durchquert, lassen Sie es uns gemeinsam tun. Verwenden Sie JavaScript, um es zu implementieren, natürlich unter Verwendung einer verketteten Speicherstruktur.

Verwenden Sie zunächst den JavaScript-Konstruktor, um einen Binärbaumknoten wie folgt zu erstellen:

function TreeNode(){
 this.data = null;//该节点数据
 this.lchild = null;//左子树
 this.rchild = null;//右子树   
};

Dann können wir durch die Binärbaumdurchquerung einen Binärbaum erstellen Algorithmus, wie folgt: Verwenden Sie die Vorbestellungssequenz, um eine Binärbaummethode zu erstellen:

/*
*method:采用先序序列建立二叉树
*@params: nodeList（Array） --树节点，以先序序列存入数组中，null代表空节点
*/
TreeNode.createBiTree = function(nodeList){
 var i = 0;
 return (function getNode(){
  var node = null,
   val = nodeList[i++];
  if(!val){
   node = null;
  }else{
   node = new TreeNode();
   node.data = val;
   node.lchild = getNode();
   node.rchild = getNode();
  }
  return node;
 })();
};

Schließlich handelt es sich um einen Binärbaum, bei dem es sich um eine Vorbestellungsdurchquerung handelt ( PreOrderTraverse) und In-Order-Traversal (InOrderTraverse) Und Post-Order-Traversal (PostOrderTraverse), wie folgt:

TreeNode.prototype = {
 constructor: TreeNode,
 _PreOrderTraverse: function(node){
  if(node){
   console.log(node.data);
   this._PreOrderTraverse(node.lchild);
   this._PreOrderTraverse(node.rchild);
  }
 },
 PreOrderTraverse: function(){
  console.log('PreOrder:');
  this._PreOrderTraverse(this);
 },
 _InOrderTraverse: function(node){
  if(node){
   this._InOrderTraverse(node.lchild);
   console.log(node.data);
   this._InOrderTraverse(node.rchild);
  }
 },
 InOrderTraverse: function(){
  console.log('InOrder:');
  this._InOrderTraverse(this);
 },
 _PostOrderTraverse: function(node){
  if(node){
   this._PostOrderTraverse(node.lchild);
   this._PostOrderTraverse(node.rchild);
   console.log(node.data);
  }
 },
 PostOrderTraverse: function(){
  console.log('PostOrder:');
  this._PostOrderTraverse(this);
 }
};

Okay, anhand des obigen Binärbaumbeispiels können wir es testen uns selbst:

var treeNode = null,
 nodeList = ['A', 'B', 'C', null, null, 'D', 'E', null, 'G', null, null, 'F', null, null, null];
//getting a binary tree from nodeList
treeNode = TreeNode.createBiTree(nodeList);
//traversing the tree of treeNode
treeNode.PreOrderTraverse();//ABCDEGF
treeNode.InOrderTraverse();//CBEGDFA
treeNode.PostOrderTraverse();//CGEFDBA

Baum

--Konzept--

Ein Baum ist eine endliche Menge von n (n>= 0) Knoten. In jedem nicht leeren Baum gibt es nur einen bestimmten Knoten, der Wurzel genannt wird. Wenn n>1 ist, können die verbleibenden Knoten in m (m>0) voneinander disjunkte Knoten unterteilt werden, von denen jeder selbst a ist Baum, Teilbaum der Wurzel genannt. Natürlich gehören Binärbäume definitiv zu Bäumen.

Das Folgende ist ein Baum (Hinweis: Die folgenden Beispiele für Bäume basieren alle auf diesem Baum):

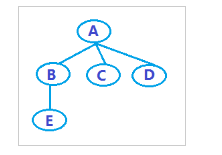Und durchqueren Sie mehr als einen Baum sind zwei häufig verwendete Durchlaufmethoden für untergeordnete Bäume, wie folgt:

1) Root-First-Durchlauf, der dem Durchlauf durch die Tiefensuche (Depth_First Search) ähnelt. Sie alle verwenden den Stapel zum Durchlaufen von Elementen wie folgt:

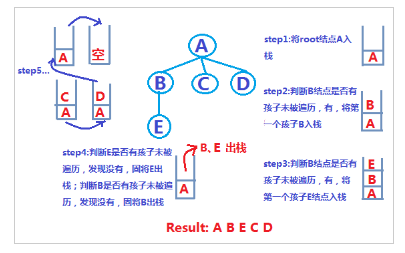2), Durchquerung nach Ebene, ähnlich der Durchquerung der Breadth_First-Suche. Sie alle verwenden Warteschlangen zum Durchlaufen von Elementen wie folgt:

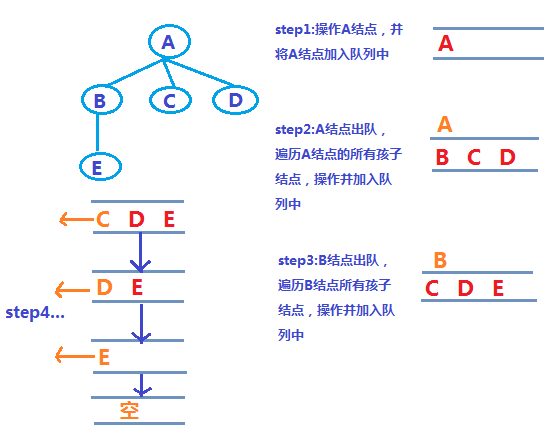Okay, jetzt, da wir den Baum und die Durchquerungsmethode verstanden haben, verwenden wir JavaScript, um ihn gemeinsam zu implementieren. Natürlich verwendet auch eine Kettenspeicherstruktur.

Verwenden Sie zunächst JavaScript, um Baumknoten wie folgt zu erstellen:

/*
*@Params: data --节点数据
   children -- 所有孩子结点
*/
function TreeNode(data, children){
 if(!(this instanceof TreeNode)){
  return new TreeNode(data, children);
 }
 this.data = data || null;
 this.children = children || [];
};

根据上述TreeNode构造函数，我们可以将例子中的树，表示如下：

var treeNode = TreeNode('A', [
       TreeNode('B', [TreeNode('E')]),
       TreeNode('C'),
       TreeNode('D')
     ]);

接着，就是编写遍历树方法咯，分别为先根遍历和按层次遍历，如下：

TreeNode.prototype = {
 constructor: TreeNode,
 _traverseAsDFS: function(node){//先根遍历
  var self = this;
  if(node){
   console.log(node.data);
   node.children.forEach(function(child){
    if(child.children.length){
     self._traverseAsDFS(child);
    }else{
     console.log(child.data);
    }
   });
  }
 },
 traverseAsDFS: function(){
  console.log('Depth_First Search');
  this._traverseAsDFS(this);
 },
 traverseAsBFS: function(){//按层次遍历
  var queue = [];
  console.log('Breadth_First Search');
  console.log(this.data);
  if(this.children.length){
   queue.push(this);
  }
  while(queue.length){
   let tempNode = queue.shift();
   tempNode.children.forEach(function(child){
    console.log(child.data);
    if(child.children.length){
     queue.push(child);
    }      
   });
  }
 }
};

好了，利用上述二叉树例子，我们可以自行测试下：

var treeNode = TreeNode('A', [
       TreeNode('B', [TreeNode('E')]),
       TreeNode('C'),
       TreeNode('D')
     ]);
treeNode.traverseAsDFS();//ABECD
treeNode.traverseAsBFS();//ABCDE

关于上述全部代码，见github。

以上就是本文的全部内容，希望本文的内容对大家的学习或者工作能带来一定的帮助，同时也希望多多支持脚本之家PHP中文网

更多Detaillierte Erläuterung der JavaScript-Baumstruktur相关文章请关注PHP中文网！