Acht Sortieralgorithmus-Praktiken

Was den Sortieralgorithmus betrifft, so wurde er in den letzten Jahren kaum verwendet. Er befindet sich grundsätzlich in einem Zustand der Nutzung und ich habe mir nie die Zeit genommen, ihn eingehend zu verstehen. Vor kurzem habe ich beschlossen, es selbst zu schreiben, um mein Verständnis zu vertiefen. Ich habe viele Informationen überprüft und viele davon wurden sehr gut analysiert, was mir geholfen hat, sie schnell zu verstehen. Vielen Dank!

1. Konzeptionelles Verständnis und Umsetzung

package com.demo.algorithm.sort; /** * 排序算法合集 * @author sheungxin * */ public class NumberSort { /** * 插入排序-直接插入排序 * 工作原理：构建有序序列，对于未排序的数据，在已排序序列中从后向前扫描，找到相应位置并插入 * 参考：http://blog.csdn.net/morewindows/article/details/6665714 * @param array * @param asc 0:升序 1:降序 */ public static void straightInsertSort(int[] array,int asc){ int tmp,n; //从第二位元素开始，第一位认为已被排序 for(int m=1;m(<)新元素，将该新元素向后移一位 for(n=m-1;n>=0&&(asc==1&&tmp>array[n]||asc==0&&tmp=)新元素或者扫描到首位时结束,将该元素插入在结束位置后面 array[n+1]=tmp; } display(array); } /** * 插入排序-希尔排序，实质就是分组排序，又称缩小增量排序 * 工作原理：先将整个待排序元素序列分割成若干个子序列(由相隔某个“增量”元素组成)分别进行直接插入排序， * 然后依次缩减增量再进行排序，待整个序列中元素基本有序(增量足够小)时，再进行一次全元素直接插入排序。 * 优势：直接插入排序在元素基本有序的情况下，效率最高 * 参考：http://blog.csdn.net/morewindows/article/details/6668714 * @param array * @param asc 0:升序 1:降序 */ public static void shellSort(int[] array,int asc){ int len=array.length; //依次缩减增量，直到增量为1 for(int gap=len/2;gap>0;gap/=2){ //根据步长把待排序元素分为gap组 for(int i=0;i(<)新元素，将该新元素向后移一位 while(k>=0&&(asc==1&&tmp>array[k]||asc==0&&tmp=)新元素或者扫描到首位时结束,将该元素插入在结束位置后面 array[k+gap]=tmp; } } } display(array); } /** * 选择排序：简单选择排序 * 原理：从无序区中选择一个最小的元素之间放到有序区的最后 * 参考：http://blog.csdn.net/morewindows/article/details/6671824 * @param array * @param asc 0:升序 1:降序 */ public static void selectSort(int[] array,int asc){ int tmp,ix; for(int i=0;iarray[j])||(asc==1&&array[ix]=0;i--){ buildHeap(array, array.length, i, asc); } //使用堆根节点构建有序序列 for(int i=array.length-1;i>=1;i--){ //依次把根节点向后交换构建有序序列 swapArray(array, 0, i); //根节点交换位置后，从0，i-1重新构建堆 buildHeap(array, i, 0, asc); } display(array); } /** * 构建二叉堆 * @param array 二叉堆数组 * @param heapSize 二叉堆大小 * @param index 当前父节点位置 * @param asc 0:升序 1:降序 */ private static void buildHeap(int[] array,int heapSize,int index,int asc){ //比较父节点、左右叶子节点，找出最大或最小节点位置 int left = index * 2 + 1; int right = index * 2 + 2; int ix=index; if(leftarray[left]||asc==0&&array[index]array[right]||asc==0&&array[ix]array[j])||(asc==1&&array[j-1]array[n]) ||(asc==1&&array[m]=tmp||asc==1&&array[j]<=tmp)){ j--; } //把右边找到的节点放到左边的空位 array[i]=array[j]; //寻找右边大于(小于)基准数的节点位置 while(i=tmp)){ i++; } //把左边找到的节点放到右边的空位 array[j]=array[i]; } //把基准数放在中间节点 array[i]=tmp; //对中间点左边的元素重复上述操作 quickSort(array, l, i-1, asc); //对中间点右边的元素重复上述操作 quickSort(array, i+1, r, asc); } display(array); } /** * 归并排序：将两个(或两个以上)有序表合并成一个新的有序表 * 原理：将序列不断拆分，再反向两两合并形成有序序列 * 时间复杂度：O(nlogn) * 参考：http://www.cnblogs.com/jingmoxukong/p/4308823.html * @param array * @param l 左指针 * @param r 右指针 * @param asc 0:升序 1:降序 */ public static void mergeSort(int[] array,int l,int r,int asc){ //找出中间点，左右拆分为两个序列 int m=(l+r)/2; if(larray[j]){ tmp[k++]=array[i++]; }else{ tmp[k++]=array[j++]; } } //把左边剩余的数移到数组中 while(i<=m){ tmp[k++]=array[i++]; } //把右边剩余的数移到数组中 while(j<=r){ tmp[k++]=array[j++]; } //把临时数组中的数覆盖原数组，形成有序集合 for(k=0;k=0;i--){ j=array[i]/((Double)Math.pow(10, d-1)).intValue()%10;//d位上的数据 tmp[count[j]-1]=array[i];//count[j]-1为第J个桶右边界的下标 count[j]--;//桶j装入数据索引减1 } //按照桶中数据顺序放入原数据序列中 for(i=0;i
        

         Nach dem Login kopieren
        
       

2. Sortieralgorithmus-Vergleichstabelle

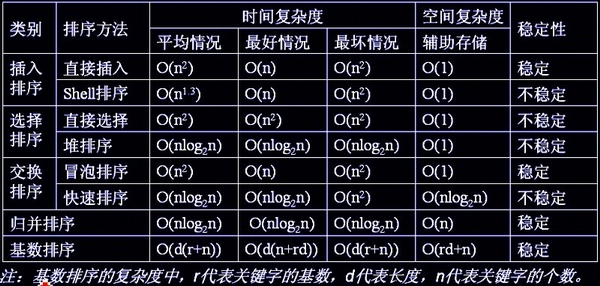
Zitat

http ://blog.csdn.net/hguisu/article/details/7776068

3. Auswahlkriterien für Sortieralgorithmen

Es gibt viele Faktoren, die die Sortierung beeinflussen, und Algorithmen mit geringer durchschnittlicher Zeitkomplexität sind es nicht Es muss das Beste sein. Umgekehrt kann für einige Sonderfälle manchmal ein Algorithmus mit einer hohen durchschnittlichen Zeitkomplexität besser geeignet sein. Gleichzeitig muss bei der Auswahl eines Algorithmus auch dessen Lesbarkeit berücksichtigt werden, um die Softwarewartung zu erleichtern. Im Allgemeinen müssen die folgenden vier Faktoren berücksichtigt werden:
1) die Größe der Anzahl n der zu sortierenden Datensätze
2) die Größe des Datenvolumens des Datensatzes selbst; die Größe des Datensatzes mit Ausnahme von Schlüsselwörtern. Die Menge anderer Informationen;
3), die Struktur und Verteilung von Schlüsselwörtern
4), die Anforderungen an die Sortierstabilität.

Angenommen, die Anzahl der zu sortierenden Elemente beträgt n
1) Wenn n groß ist, sollte eine Sortiermethode mit einer Zeitkomplexität von O(nlog2n) verwendet werden: schnelle Sortierung, Heap-Sortierung oder Zusammenführung Sortierreihenfolge.
a. Schnelle Sortierung: Dies gilt derzeit als die beste Methode zur internen Sortierung, wenn die zu sortierenden Schlüsselwörter zufällig verteilt sind.
b. Wenn der Speicherplatz es zulässt und Stabilität erforderlich ist; wird die Effizienz verbessern. Verbessert.
2), wenn n groß ist, ist genügend Speicherplatz vorhanden und Stabilität ist erforderlich => Zusammenführungssortierung
3), wenn n klein ist, kann direkte Einfügung oder direkte Auswahlsortierung verwendet werden.
a. Direkte Einfügungssortierung: Wenn die Elemente in der richtigen Reihenfolge verteilt werden, verringert die direkte Einfügungssortierung die Anzahl der Vergleiche und die Anzahl der verschobenen Datensätze erheblich.
b. Wenn keine Stabilität erforderlich ist, wählen Sie Direktauswahlsortierung
4). Die herkömmliche Blasensortierung wird im Allgemeinen nicht oder nicht direkt verwendet.
5) Radix-Sortierung: Es handelt sich um einen stabilen Sortieralgorithmus, der jedoch bestimmte Einschränkungen aufweist:
Die Anzahl der aufgezeichneten Schlüsselwortziffern ist gering.
c. Wenn es sich um eine Zahl handelt, ist es am besten, sie ohne Vorzeichen zu verwenden, da sonst die entsprechende Zuordnungskomplexität zunimmt. Sie können die positiven und negativen Zahlen zuerst separat sortieren.


Zitat

http://blog.csdn.net/hguisu/article/details/7776068