Aufbau eines Drohnennavigationssystems mit Matplotlib und A*-Algorithmus

Haben Sie sich jemals gefragt, wie Drohnen durch komplexe Umgebungen navigieren? In diesem Blog erstellen wir ein einfaches Drohnennavigationssystem mit Python, Matplotlib und dem A*-Algorithmus. Am Ende haben Sie ein funktionierendes System, das eine Drohne visualisiert, die ein Labyrinth löst!

Was Sie lernen werden

1. Grundlegende KI-Terminologien wie „Agent“ und „Umgebung“.
2. Wie man mit Python ein Labyrinth erstellt und visualisiert.
3. Wie der A*-Algorithmus funktioniert, um Navigationsprobleme zu lösen.
4. So implementieren und visualisieren Sie den Flugweg der Drohne.

Einführung

Um unser Drohnen-Navigationssystem aufzubauen, benötigen wir Folgendes:

1. Ein Agent:Die Drohne?.
2. Ein Pfad: Ein 2D-Labyrinth, durch das die Drohne navigiert ?️.
3. Ein Suchalgorithmus:Der A*-Algorithmus ⭐.

Aber lassen Sie uns zunächst kurz einige grundlegende KI-Begriffe für diejenigen durchgehen, die neu sind.

Wichtige KI-Begriffe

• Agent: Eine Entität (wie unsere Drohne), die ihre Umgebung (Labyrinth) wahrnimmt und Maßnahmen ergreift, um ein Ziel zu erreichen (das Ende des Labyrinths zu erreichen).
• Umgebung: Die Welt, in der der Agent tätig ist, hier dargestellt als 2D-Labyrinth.
• Heuristik: Eine Faustregel oder eine Schätzung, die als Leitfaden für die Suche dient (z. B. das Messen der Entfernung zum Ziel).

Das Systemdesign

Unsere Drohne navigiert durch ein 2D-Labyrinth. Das Labyrinth besteht aus:

• Wände (unpassierbare Bereiche, dargestellt durch 1s).
• Pfade (offene Räume werden durch Nullen dargestellt).

Die Ziele der Drohne:

1. Wände vermeiden.?
2. Das Ende des Weges erreichen.?

So sieht das Labyrinth aus:

Schritt 1: Aufbau des Labyrinths

Erforderliche Bibliotheken importieren

Zuerst installieren und importieren Sie die erforderlichen Bibliotheken:

import matplotlib.pyplot as plt
import numpy as np
import random
import math
from heapq import heappop, heappush

Labyrinthabmessungen definieren

Lassen Sie uns die Größe des Labyrinths definieren:
Python
BREITE, HÖHE = 22, 22

Richtungen und Gewichte festlegen

In der realen Navigation kann die Bewegung in verschiedene Richtungen unterschiedliche Kosten verursachen. Beispielsweise könnte es schwieriger sein, nach Norden zu ziehen als nach Osten.

DIRECTIONAL_WEIGHTS = {'N': 1.2, 'S': 1.0, 'E': 1.5, 'W': 1.3}
DIRECTIONS = {'N': (-1, 0), 'S': (1, 0), 'E': (0, 1), 'W': (0, -1)}

Initialisieren Sie das Labyrinthgitter

Wir beginnen mit einem Gitter, das mit Wänden (1s) gefüllt ist:

import matplotlib.pyplot as plt
import numpy as np
import random
import math
from heapq import heappop, heappush

Der Numpy. Die Funktion ones() wird verwendet, um ein neues Array mit einer bestimmten Form und einem bestimmten Typ zu erstellen, das mit Einsen gefüllt ist. Dies ist hilfreich beim Initialisieren eines Arrays mit Standardwerten.

Schritt 2: Das Labyrinth schnitzen

Jetzt definieren wir eine Funktion, die Wege in Ihrem Labyrinth „ausschneidet“, das gerade mit nur Wänden initialisiert ist

DIRECTIONAL_WEIGHTS = {'N': 1.2, 'S': 1.0, 'E': 1.5, 'W': 1.3}
DIRECTIONS = {'N': (-1, 0), 'S': (1, 0), 'E': (0, 1), 'W': (0, -1)}

Start- und Endpunkte definieren

maze = np.ones((2 * WIDTH + 1, 2 * HEIGHT + 1), dtype=int)

Schritt 3: Visualisierung des Labyrinths

Verwenden Sie Matplotlib, um das Labyrinth anzuzeigen:

def carve(x, y):
    maze[2 * x + 1, 2 * y + 1] = 0  # Mark current cell as a path
    directions = list(DIRECTIONS.items())
    random.shuffle(directions)  # Randomize directions

    for _, (dx, dy) in directions:
        nx, ny = x + dx, y + dy
        if 0 <= nx < WIDTH and 0 <= ny < HEIGHT and maze[2 * nx + 1, 2 * ny + 1] == 1:
            maze[2 * x + 1 + dx, 2 * y + 1 + dy] = 0
            carve(nx, ny)

carve(0, 0)  # Start carving from the top-left corner

Schritt 4: Das Labyrinth mit A lösen*

Der A*-Algorithmus findet den kürzesten Weg in einem gewichteten Labyrinth mithilfe einer Kombination aus Pfadkosten und Heuristik.

Definieren Sie die Heuristik

Wir verwenden die Euklidische Distanz als unsere Heuristik:

start = (1, 1)
end = (2 * WIDTH - 1, 2 * HEIGHT - 1)
maze[start] = 0
maze[end] = 0

A*-Algorithmus-Implementierung

fig, ax = plt.subplots(figsize=(8, 6))
ax.imshow(maze, cmap='binary', interpolation='nearest')
ax.set_title("2D Maze")
plt.show()

Schritt 5: Visualisierung der Lösung

Wir haben das Labyrinth, aber Sie können den Weg der Drohne noch nicht sehen.
Lassen Sie uns den Weg der Drohne visualisieren:

def heuristic(a, b):
    return math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)

Fazit

Herzlichen Glückwunsch! ? Sie haben ein funktionierendes Drohnen-Navigationssystem gebaut, das:

• Erzeugt ein 2D-Labyrinth.
• Löst das Problem mit dem A*-Algorithmus.
• Visualisiert den kürzesten Weg.

Nächste Schritte

1. Experimentieren Sie mit verschiedenen Labyrinthgrößen und -gewichten.
2. Versuchen Sie es mit anderen Heuristiken wie der Manhattan-Distanz.
3. Visualisieren Sie ein 3D-Labyrinth für mehr Komplexität!

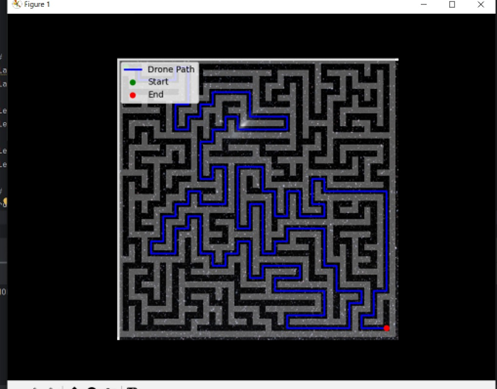
Teilen Sie Ihre Ergebnisse gerne mit uns oder stellen Sie Fragen in den Kommentaren unten.
Bis ins Unendliche und darüber hinaus?

Das obige ist der detaillierte Inhalt vonAufbau eines Drohnennavigationssystems mit Matplotlib und A*-Algorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!