Metriken für Regressionsalgorithmen

Fehlermetriken für Regressionsalgorithmen

Wenn wir einen Regressionsalgorithmus erstellen und wissen möchten, wie effizient dieses Modell war, verwenden wir Fehlermetriken, um Werte zu erhalten, die den Fehler unseres maschinellen Lernmodells darstellen. Die Metriken in diesem Artikel sind wichtig, wenn wir den Fehler von Vorhersagemodellen für numerische Werte (reelle Zahlen, ganze Zahlen) messen möchten.

In diesem Artikel behandeln wir die wichtigsten Fehlermetriken für Regressionsalgorithmen, führen die Berechnungen manuell in Python durch und messen den Fehler des maschinellen Lernmodells an einem Dollar-Kursdatensatz.

Behandelte Metriken

• SE – Fehlersumme
• ME – Mittlerer Fehler
• MAE – Mittlerer absoluter Fehler
• MPE – Mittlerer prozentualer Fehler
• MAPAE – Mittlerer absoluter prozentualer Fehler

Beide Metriken sind ein wenig ähnlich, wobei wir Metriken für den Durchschnitt und den Prozentsatz des Fehlers und Metriken für den durchschnittlichen und absoluten Prozentsatz des Fehlers haben, differenziert, nur dass eine Gruppe den tatsächlichen Wert der Differenz und die andere den absoluten Wert erhält des Unterschieds. Es ist wichtig zu bedenken, dass bei beiden Kennzahlen unsere Prognose umso besser ist, je niedriger der Wert ist.

SE – Fehlersumme

Die SE-Metrik ist die einfachste von allen in diesem Artikel, deren Formel lautet:

SE = εR — P

Daher ist es die Summe der Differenz zwischen dem realen Wert (Zielvariable des Modells) und dem vorhergesagten Wert. Diese Metrik hat einige negative Punkte, wie zum Beispiel, dass Werte nicht als absolut behandelt werden, was folglich zu einem falschen Wert führt.

ME – Mittelwert des Fehlers

Die ME-Metrik ist eine „Ergänzung“ der SE, wobei wir grundsätzlich den Unterschied haben, dass wir einen Durchschnitt der SE aufgrund der Anzahl der Elemente erhalten:

ME = ε(R-P)/N

Im Gegensatz zu SE teilen wir das SE-Ergebnis einfach durch die Anzahl der Elemente. Diese Metrik hängt wie SE vom Maßstab ab, das heißt, wir müssen denselben Datensatz verwenden und können ihn mit verschiedenen Prognosemodellen vergleichen.

MAE – Mittlerer absoluter Fehler

Die MAE-Metrik ist die ME, berücksichtigt jedoch nur absolute (nicht negative) Werte. Wenn wir die Differenz zwischen tatsächlich und vorhergesagt berechnen, erhalten wir möglicherweise negative Ergebnisse und diese negative Differenz wird auf frühere Messwerte angewendet. Bei dieser Metrik müssen wir die Differenz in positive Werte umwandeln und dann den Durchschnitt basierend auf der Anzahl der Elemente bilden.

MPE – Mittlerer prozentualer Fehler

Die MPE-Metrik ist der durchschnittliche Fehler als Prozentsatz der Summe jeder Differenz. Hier müssen wir den Prozentsatz der Differenz nehmen, ihn addieren und ihn dann durch die Anzahl der Elemente dividieren, um den Durchschnitt zu erhalten. Daher wird die Differenz zwischen dem tatsächlichen Wert und dem vorhergesagten Wert gebildet, durch den tatsächlichen Wert dividiert, mit 100 multipliziert, wir addieren den gesamten Prozentsatz und dividieren ihn durch die Anzahl der Elemente. Diese Metrik ist unabhängig vom Maßstab (%).

MAPAE – Mittlerer absoluter prozentualer Fehler

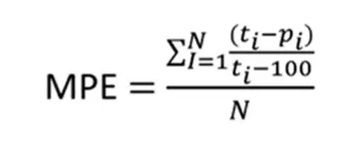
Die MAPAE-Metrik ist der vorherigen Metrik sehr ähnlich, aber die Differenz zwischen vorhergesagtem x tatsächlichem Wert wird absolut gemacht, das heißt, Sie berechnen sie mit positiven Werten. Daher ist diese Metrik die absolute Differenz im Fehlerprozentsatz. Diese Metrik ist auch skalenunabhängig.

Metriken in der Praxis nutzen

Anhand einer Erläuterung jeder Metrik berechnen wir beide manuell in Python basierend auf einer Vorhersage aus einem maschinellen Lernmodell für den Dollar-Wechselkurs. Derzeit liegen die meisten Regressionsmetriken in vorgefertigten Funktionen im Sklearn-Paket vor, wir werden sie hier jedoch nur zu Lehrzwecken manuell berechnen.

Wir werden die Algorithmen RandomForest und Decision Tree nur verwenden, um die Ergebnisse zwischen den beiden Modellen zu vergleichen.

Datenanalyse

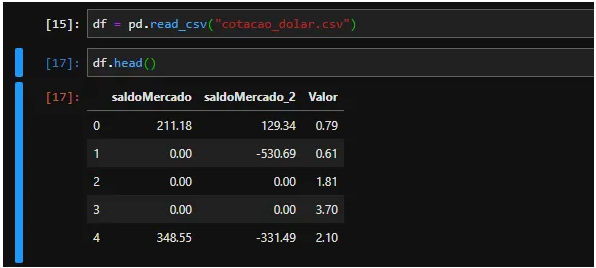
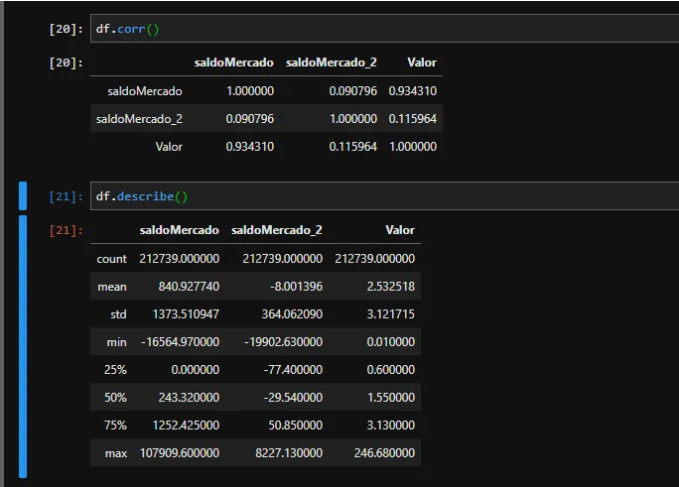
In unserem Datensatz haben wir eine Spalte mit SaldoMercado und saldoMercado_2, bei denen es sich um Informationen handelt, die die Spalte „Wert“ (unser Dollarkurs) beeinflussen. Wie wir sehen können, hat der MercadoMercado-Saldo eine engere Beziehung zum Angebot als der Merado_2-Saldo. Es ist auch möglich zu beobachten, dass wir keine fehlenden Werte haben (unendliche oder Nan-Werte) und dass die Spalte balanceMercado_2 viele nicht absolute Werte enthält.

Modellvorbereitung

Wir bereiten unsere Werte für das maschinelle Lernmodell vor, indem wir die Prädiktorvariablen und die Variable definieren, die wir vorhersagen möchten. Wir verwenden train_test_split, um die Daten zufällig in 30 % zum Testen und 70 % zum Training aufzuteilen.

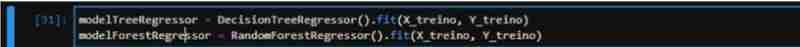
Schließlich initialisieren wir beide Algorithmen (RandomForest und DecisionTree), passen die Daten an und messen die Punktzahl beider mit den Testdaten. Wir haben eine Punktzahl von 83 % für TreeRegressor und 90 % für ForestRegressor erhalten, was theoretisch darauf hindeutet, dass ForestRegressor eine bessere Leistung erbracht hat.

Ergebnisse und Analyse

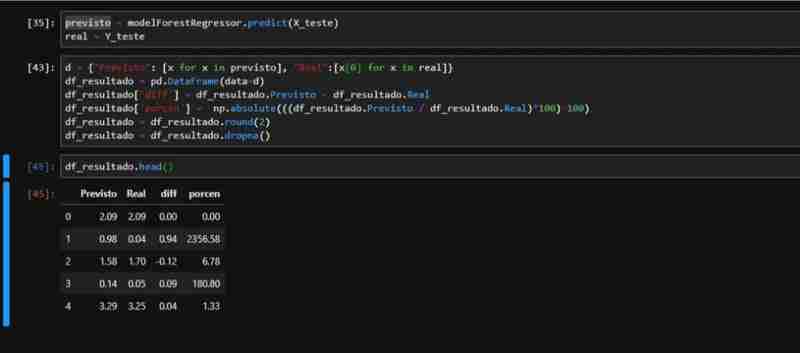
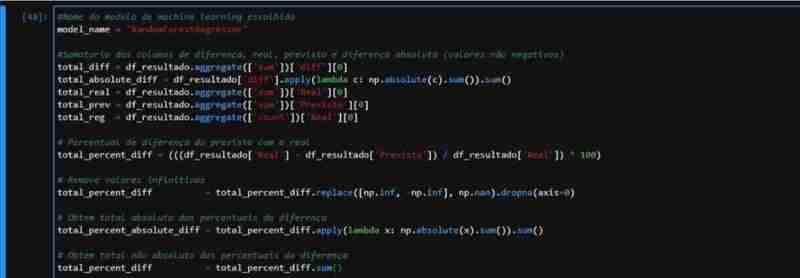
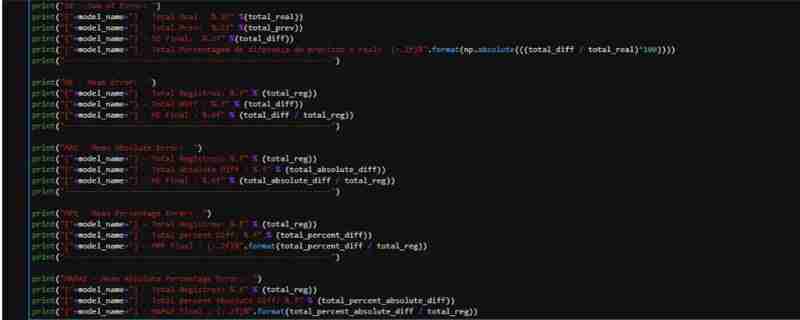
Angesichts der teilweise beobachteten Leistung von ForestRegressor haben wir einen Datensatz mit den notwendigen Daten erstellt, um die Metriken anzuwenden. Wir führen die Vorhersage anhand der Testdaten durch und erstellen einen DataFrame mit den tatsächlichen und vorhergesagten Werten, einschließlich Spalten für Differenz und Prozentsatz.

Wir können Folgendes im Verhältnis zum tatsächlichen Gesamtkurs des Dollars im Vergleich zu dem von unserem Modell vorhergesagten Kurs beobachten:

• Wir hatten eine Gesamtdifferenz von 578,00 R$
• Dies entspricht einer Differenz von 0,36 % zwischen vorhergesagten x tatsächlichen Werten (nicht als absolute Werte berücksichtigt)
• In Bezug auf den durchschnittlichen Fehler (ME) hatten wir einen niedrigen Wert, einen Durchschnitt von 0,009058 R$
• Für den absoluten Durchschnitt steigt dieser Wert etwas an, da wir negative Werte in unserem Datensatz haben

Ich betone, dass wir die Berechnung hier zu Lehrzwecken manuell durchführen. Es wird jedoch empfohlen, die Metrikfunktionen aus dem Sklearn-Paket zu verwenden, da die Leistung besser ist und die Fehlerwahrscheinlichkeit bei der Berechnung geringer ist.

Der vollständige Code ist auf meinem GitHub verfügbar: github.com/AirtonLira/artigo_metricasregressao

Autor: Airton Lira Junior

LinkedIn: LinkedIn.com/in/airton-lira-junior-6b81a661/

Das obige ist der detaillierte Inhalt vonMetriken für Regressionsalgorithmen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!