Ein bedeutender Durchbruch in der Riemann-Hypothese! Tao Zhexuan empfiehlt dringend neue Arbeiten vom MIT und Oxford, und der 37-jährige Fields-Medaillengewinner nahm daran teil

Vor kurzem hat die Riemann-Hypothese, bekannt als eines der sieben großen Probleme des Jahrtausends, einen neuen Durchbruch erzielt.

Die Riemann-Hypothese ist ein sehr wichtiges ungelöstes Problem in der Mathematik, das sich auf die genauen Eigenschaften der Verteilung von Primzahlen bezieht (Primzahlen sind Zahlen, die nur durch 1 teilbar sind, und sie selbst spielen dabei eine grundlegende Rolle Zahlentheorie Rolle).

In der heutigen mathematischen Literatur gibt es mehr als tausend mathematische Sätze, die auf der Aufstellung der Riemann-Hypothese (oder ihrer verallgemeinerten Form) basieren. Mit anderen Worten: Sobald die Riemann-Hypothese und ihre verallgemeinerte Form bewiesen sind, werden diese mehr als tausend Sätze als Theoreme etabliert, die einen tiefgreifenden Einfluss auf das Gebiet der Mathematik haben werden, und wenn sich die Riemann-Hypothese als falsch erweist, dann unter anderem Auch diese Sätze werden teilweise ihre Gültigkeit verlieren.

Der neue Durchbruch geht auf einen Artikel des MIT-Mathematikprofessors Larry Guth und des Oxford University Institute of Mathematics-Professors und Fields-Medaillengewinners James Maynard zurück. Der Mathematiker Terence Tao, der die Arbeit empfohlen hat, sagte, dass sie die erste wesentliche Verbesserung gegenüber der klassischen Ingham-Schranke von 1940 für die Nullstellen der Riemannschen Zeta-Funktion (und allgemeiner für die Kontrolle großer Werte verschiedener Dirichlet-Reihen) darstellten. Zuvor hinderte die Ingham-Schranke, die vor mehr als 80 Jahren eingeführt wurde, Mathematiker aufgrund fehlender Verbesserungen daran, viele Dinge in der analytischen Zahlentheorie zu tun.

Allerdings sagte Tao Zhexuan auch, dass dies zwar ein bedeutender Durchbruch sei, aber noch weit von der vollständigen Lösung der Riemann-Hypothese entfernt sei und daher rational betrachtet werden sollte.

Was ist die Riemann-Hypothese?

Die Riemann-Hypothese oder Riemann-Hypothese wurde 1859 vom deutschen Mathematiker Bernhard Riemann vorgeschlagen. Diese Vermutung steht in engem Zusammenhang mit der Verteilung von Primzahlen und ihr Kerninhalt betrifft die nichttrivialen Nullstellen der Riemannschen Zeta-Funktion.

^{Bernhard Riemann, Quelle: Facts.net/}

Der Inhalt der Riemann-Hypothese kann nicht durch völlig elementare Mathematik beschrieben werden. Grob gesagt handelt es sich um eine Vermutung für eine komplexe Variablenfunktion namens Riemannsche Zeta-Funktion (d. h. eine Funktion, bei der sowohl die Variable als auch der Funktionswert Werte im komplexen Bereich annehmen können). Die Riemannsche Zetafunktion hat wie viele andere Funktionen an einigen Punkten den Wert Null. Diese Punkte werden als Nullpunkte der Riemannschen Zetafunktion bezeichnet. Unter diesen Nullstellen gibt es einige besonders wichtige nichttriviale Nullstellen, die sogenannte Riemannsche Zetafunktion. Was die Riemann-Hypothese vermutet, ist, dass alle nicht trivialen Nullpunkte auf einer speziellen geraden Linie verteilt sind, die als „kritische Linie“ bezeichnet wird (zitiert aus dem Blog des populärwissenschaftlichen Autors Lu Changhai).

Die Riemannsche ζ-Funktion ist definiert als:

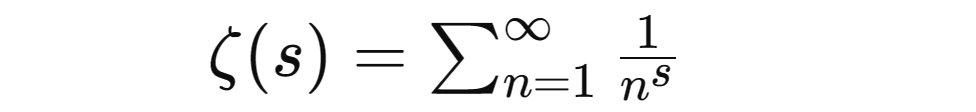
Die Riemannsche Hypothese besagt, dass der Realteil aller nicht trivialen Nullstellen der ζ-Funktion 1/2 beträgt. Das heißt, wenn ζ(s)=0 und s eine nicht triviale Nullstelle ist (d. h. s ist nicht gerade negativ), dann sollte der Realteil von s 1/2 sein.

Die Riemann-Hypothese ist heute das wichtigste und am meisten erwartete mathematische Problem der Welt. Wenn die Vermutung wahr ist, kann die Verteilung der Primzahlen unter den natürlichen Zahlen genau beschrieben werden, und sie wird weitreichende Anwendung und Einfluss auf die Lösung der Zahlentheorie, der komplexen Analysis und anderer Zweige der Mathematik haben.

Bisher sind 165 Jahre vergangen, seit die Riemann-Hypothese aufgestellt wurde. Es gab viele Studien, die versuchten, die Riemann-Hypothese zu beweisen, aber alle führten zu nichts.

Versuche, die Riemann-Hypothese zu lösen

Seit der Vorschlag der Riemann-Hypothese haben viele Mathematiker begonnen, den Beweis zu erforschen.

Im Jahr 1896 bewiesen die französischen Mathematiker Jacques Adamard und Charles Jean de la Vallée-Poussin unabhängig voneinander, dass es auf einer Geraden keine Nullpunkte gibt. Zusammen mit anderen Eigenschaften, die Riemann für nicht triviale Nullstellen bewiesen hatte, zeigt dies, dass alle nicht trivialen Nullstellen auf Regionen liegen müssen. Dies ist ein entscheidender Schritt im ersten vollständigen Beweis des Primzahlsatzes.

Im Jahr 1900 nahm David Hilbert, ein deutscher Mathematiker und einer der Väter der modernen Mathematik, die Riemann-Hypothese in seine berühmten 23 Fragen auf und zusammen mit Goldbachs Hypothese bildeten sie Hilberts Listenfrage Nr. 8. Gleichzeitig ist die Riemann-Hypothese auch das einzige Hilbert-Problem, das in den Millennium-Preis des Clay Mathematics Institute aufgenommen wurde.

Im Jahr 1914 bewies der britische Mathematiker Godfrey Harold Hardy, dass es auf der Geraden unendlich viele Nullpunkte gibt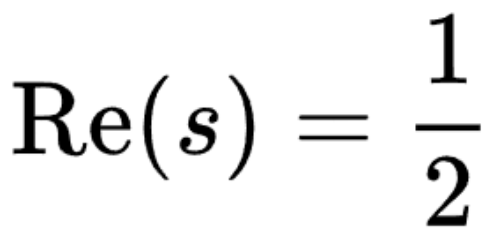. Später bestand die Arbeit von Hardy und dem britischen Mathematiker John Unther Littlewood im Jahr 1921 und Selberg im Jahr 1942 (Theorem über die kritische Linie) darin, die durchschnittliche Dichte von Nullpunkten auf der kritischen Linie zu berechnen.

Bis in die letzten Jahre sorgten Versuche, die Riemann-Hypothese zu beweisen, oft für Aufsehen.

Im September 2018 erregte eine beispiellose Rede in Heidelberg den MathematikzirkelDer Beweis der Riemann-Hypothese des 89-jährigen Sir Atiyah erregte weltweite Aufmerksamkeit. Im Rampenlicht verbrachte Sir Atiyah 45 Minuten damit, der Welt den Beweis dieser mathematischen Vermutung vorzustellen, die eine mehr als 150-jährige Geschichte hat.

Aber Sir Atiyahs Beweis ist nur die folgende Seite der PPT. Ein solcher Beweis scheint nicht überzeugend. Auf die Frage, ob er die Riemann-Hypothese gelöst habe, antwortete er: „Das hängt von Ihrer Logik ab. Ich habe die ursprüngliche Riemann-Hypothese bewiesen, es sei denn, Sie sind der Typ Mathematiker, der Beweise durch Widerspruch nicht akzeptiert.“ hat nicht alle Probleme gelöst, und es wird in Zukunft noch viele Probleme geben. Er hat nur den ersten Schritt getan (der erste Schritt ist die Lösung).

Leider istSir Atiyah im Januar 2019 verstorben.

Jetzt hat jemand die Riemann-Hypothese in Frage gestellt.

Was Guth und Maynard taten

Zu Guths und Maynards neuem Durchbruch kommentierte die bekannte Mathematikerin Teresa Tao: „Guth und Maynard haben beim Studium der Riemann-Hypothese wichtige Fortschritte gemacht, obwohl sie noch weit davon entfernt sind, diese lange zu lösen.“ -stehendes Problem. Mathematikprobleme haben noch einen langen Weg vor sich Der Mathematiker Albert Ingham hat um 1940 wesentliche Verbesserungen an den klassischen Grenzen der Nullstellen der Riemannschen Zeta-Funktion (und allgemeiner an großen Werten für verschiedene Dirichlet-Reihen) vorgenommen.

Im Jahr 1940 schlug der Mathematiker Albert Ingham eine Grenze zur Beschreibung dieser Nullpunkte vor, die damals die Grundlage für die theoretische Forschung bildete. Bis zur Arbeit von Guth und Maynard war diese Grenze jedoch kaum verfeinert worden. Die Forschung von Guth und Maynard verbesserte nicht nur diese Schranke von Ingham, sondern ihre Methode lieferte auch neue Werkzeuge und Perspektiven für den Umgang mit großen Werten von Dirichlet-Reihen, die für viele zahlentheoretische und analytische Probleme wichtig sind.

Dieser Artikel beweist eine neue Grenze für die Häufigkeit großer Werte von Dirichlet-Polynomen. Dies liefert eine verbesserte Schätzung für ein Dirichlet-Polynom der Länge N mit Werten nahe

. Darüber hinaus leitet die Studie eine Nullpunktdichteschätzung

und einen asymptotischen Ausdruck für Primzahlen über kurze Längenintervalle

ab.

Tao Zhexuan selbst gab aus mathematischer Sicht einige Erklärungen zu dieser Forschung. Sei ?(σ,?) die Anzahl der Nullstellen der Riemannschen ζ-Funktion, wobei der Realteil mindestens σ und der Imaginärteil höchstens T beträgt. Die Riemann-Hypothese sagt uns, dass N (σ,?) für jedes σ>1/2 verschwinden wird, aber diese Hypothese kann noch nicht bewiesen werden. Aber als zweitbeste Option können Mathematiker eine Nullpunktdichteschätzung nachweisen, die eine nicht triviale Obergrenze für ?(σ,?) darstellt.

Es stellt sich heraus, dass σ=3/4 ein Schlüsselwert ist. Im Jahr 1940 leitete Ingham die Schranke ?(3/4,?)≪?(3/5+?(1)) ab.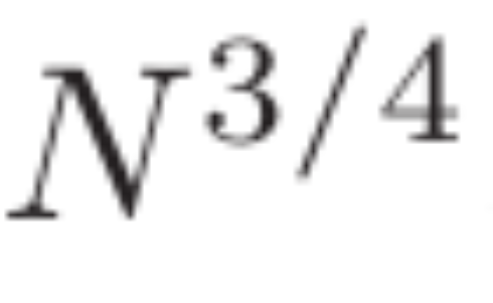

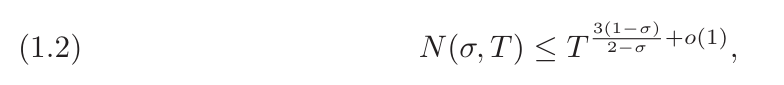
In den nächsten achtzig Jahren waren Verbesserungen an dieser Grenze nur geringfügige Verfeinerungen des ?(1)-Fehlers. Dies schränkt Forscher bei der Durchführung eingehenderer Forschungen in der analytischen Zahlentheorie ein: Um beispielsweise in fast allen kurzen Intervallen der Form (?,?+?^?) einen guten Primzahlsatz zu erhalten, waren die Menschen lange Zeit eingeschränkt bis ?>1/6 liegt das Haupthindernis in der fehlenden Verbesserung der Ingham-Grenzen.

Guth und Maynard haben schließlich die Ingham-Grenze von 3/5=0,6 auf 13/25=0,52 verbessert. Dies hat zu vielen entsprechenden Verbesserungen in der analytischen Zahlentheorie geführt. Beispielsweise können Forscher den Bereich des Primzahlsatzes in fast jedem kurzen Intervall beweisen, jetzt von θ>1/6=0,166… bis θ>2/15=0,133…

Über den Autor

Larry Guth ist seit Juli 2019 Claude E. Shannon-Professor für Mathematik am MIT und wurde 2021 zum MacVicar Fellow gewählt.

Er promovierte 2005 am MIT unter der Leitung von Tom Mrowka. Es folgten ein Postdoc-Aufenthalt an der Stanford University, eine Juniorfakultätsstelle an der University of Toronto und 2011 die Ernennung zum Courant Institute Professor. Anschließend wechselte er 2012 als Professor an die Fakultät für Mathematik des MIT.

Guths Forschungsinteressen sind metrische Geometrie, harmonische Analyse und Extremwertkombinationen. Unter metrischer Geometrie versteht man die Untersuchung von Ungleichungen in Bezug auf Länge, Fläche und Volumen. Einige wichtige Beispiele sind isoperimetrische Ungleichungen und Kontraktionsungleichungen. Kontraktionsungleichungen bildeten einen Schwerpunkt von Guths Arbeit, ein weiterer Schwerpunkt lag auf der Suche nach Zusammenhängen zwischen geometrischen Ungleichungen und der Topologie.

Vor kurzem beschäftigt sich Guth mit der Forschung zur harmonischen Analyse und Kombinatorik. Viele Arbeiten beziehen sich auf das Kakeya-Problem, ein ungelöstes Problem in der euklidischen Geometrie, auf Schätzungen vom eingeschränkten Typ in der Fourier-Analyse und auf Schätzungen von Linienvorkommensraten in der extremen Kombinatorik.

^{, ist ein britischer Mathematiker, dessen Forschungsgebiet die analytische Zahlentheorie, insbesondere die Primzahlentheorie, ist.}

Einige der bekanntesten Probleme der Zahlentheorie beziehen sich auf die Verteilung von Primzahlen. Während die großräumige Verteilung von Primzahlen den Sätzen der Zahlentheorie (genauer gesagt der Riemann-Hypothese) folgt, müssen sich viele natürliche Probleme mit kurzen (oder spärlichen) Skalen befassen.

James Maynard erzielte 2013 wichtige Ergebnisse zur Primzahlzwillingsvermutung. Er bewies, dass es unendlich viele Primzahlpaare mit Intervallen von weniger als 600 gibt. Dieses Ergebnis ist kleiner als die 70 Millionen Intervalle von Zhang Yitang. Obwohl seine Arbeit ein halbes Jahr später als Zhang Yitang veröffentlicht wurde, wurden seine Ergebnisse von Experten der Zahlentheorie hoch gelobt.

Tao Zhexuan kommentierte: „Um ehrlich zu sein, ist seine Art zu beschreiben tatsächlich klarer als meine … Es stellt sich heraus, dass seine Aussage etwas stärker ist.“

Maynards Methode ist auf schockierende Weise sowohl elegant als auch kraftvoll durchbricht die Grenzen der Screening-Theorie. Und in einer scheinbar entgegengesetzten Richtung zeigte er weiter, dass Primzahlen manchmal viel spärlicher als der Durchschnitt sind, ein berühmtes Erdős-Problem, das seit Jahrzehnten keine wesentlichen Fortschritte gemacht hatte.

Maynard leistete auch grundlegende Arbeit auf dem Gebiet der diophantischen Näherung und löste die Duffin-Schaeffer-Vermutung zusammen mit Koukoulopoulos, einem Professor für Mathematik an der Universität Montreal. Diese 1941 aufgestellte Vermutung kann als endgültige Verallgemeinerung des Satzes von Khintchine betrachtet werden, der beschreibt, wie eine typische reelle Zahl durch eine rationale Zahl angenähert werden kann.

Im Jahr 2022 wurde Maynard für seine Beiträge zur analytischen Zahlentheorie mit der Fields-Medaille ausgezeichnet. Die Fields-Medaille ist die prestigeträchtigste Auszeichnung in der Mathematik und wird oft als Nobelpreis für Mathematik angesehen. James Maynard wird für seine Beiträge zur analytischen Zahlentheorie geehrt, die zu bedeutenden Fortschritten beim Verständnis der Struktur von Primzahlen und der diophantischen Näherung geführt haben.

Im Jahr 2023 gewann er einen weiteren New Horizons Award in Mathematik.

Ich freue mich darauf, dass die beiden Mathematiker bei Weltproblemen wie der Riemann-Hypothese weitere Fortschritte machen.

Referenzlink:

https://www.jiqizhixin.com/articles/2019-01-12

^{https://www.zhihu.com/tardis/zm/ art/557594612}

^{https://news.mit.edu/2014/profile-larry-guth-0527}

^{https://mathstodon.xyz/@tao/112557248794707738}

^{https://zh.wikipedia.org/wiki/% E9% BB%8E% EBC%9% EBC%8% 9C% E6%83% B3}

Das obige ist der detaillierte Inhalt vonEin bedeutender Durchbruch in der Riemann-Hypothese! Tao Zhexuan empfiehlt dringend neue Arbeiten vom MIT und Oxford, und der 37-jährige Fields-Medaillengewinner nahm daran teil. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!