
Eine rekursive Methode ist eine Methode, die sich selbst aufruft. Viele mathematische Funktionen werden durch Rekursion definiert. Beginnen wir mit einem einfachen Beispiel. Die Fakultät einer Zahl n kann wie folgt rekursiv definiert werden:
0! = 1;
N! = n × (n - 1)!; n > 0
Wie findet man n! für ein gegebenes n? 1! zu finden ist einfach, weil Sie wissen, dass 0! 1 ist und 1! 1 × 0 ist !. Vorausgesetzt, dass Sie (n - 1)! kennen, können Sie n! sofort erhalten, indem Sie n × (n - 1)! verwenden. Somit wird das Problem der Berechnung von n! auf die Berechnung von (n - 1)! reduziert. Bei der Berechnung von (n - 1)! können Sie dieselbe Idee rekursiv anwenden, bis n auf 0 reduziert wird.
Es sei Fakultät(n) die Methode zur Berechnung von n!. Wenn Sie die Methode mit n = 0 aufrufen, gibt sie sofort das Ergebnis zurück. Die Methode weiß den einfachsten Fall zu lösen, der als Basisfall oder Stoppbedingung bezeichnet wird. Wenn Sie die Methode mit n > 0 reduziert es das Problem in ein Teilproblem zur Berechnung der Fakultät von n - 1. Das Teilproblem ist im Wesentlichen dasselbe wie das ursprüngliche Problem, aber es ist einfacher oder kleiner. Da das Unterproblem dieselben Eigenschaften wie das ursprüngliche Problem hat, können Sie die Methode mit einem anderen Argument aufrufen, was als rekursiver Aufruf bezeichnet wird.
Der rekursive Algorithmus zur Berechnung von Fakultät(n) kann einfach wie folgt beschrieben werden:
wenn (n == 0)
return 1;
sonst
return n * Faculty(n - 1);
Ein rekursiver Aufruf kann zu vielen weiteren rekursiven Aufrufen führen, da die Methode ein Teilproblem immer wieder in neue Teilprobleme aufteilt. Damit eine rekursive Methode beendet wird, muss das Problem schließlich auf einen Stoppfall reduziert werden, an dem die Methode ein Ergebnis an ihren Aufrufer zurückgibt. Der Aufrufer führt dann eine Berechnung durch und gibt das Ergebnis an seinen eigenen Aufrufer zurück. Dieser Vorgang wird fortgesetzt, bis das Ergebnis an den ursprünglichen Aufrufer zurückgegeben wird. Das ursprüngliche Problem kann nun durch Multiplikation von n mit dem Ergebnis von Fakultät(n - 1) gelöst werden.
Der folgende Code stellt ein vollständiges Programm dar, das den Benutzer zur Eingabe einer nichtnegativen Ganzzahl auffordert und die Fakultät für die Zahl anzeigt.

Die Methode Fakultät (Zeilen 17–22) ist im Wesentlichen eine direkte Übersetzung der rekursiven mathematischen Definition für die Fakultät in Java-Code. Der Aufruf von factorial ist rekursiv, da er sich selbst aufruft. Der an factorial übergebene Parameter wird dekrementiert, bis er den Basisfall von 0 erreicht.
Sie sehen, wie man eine rekursive Methode schreibt. Wie funktioniert Rekursion hinter den Kulissen? Die folgende Abbildung zeigt die Ausführung der rekursiven Aufrufe, beginnend mit n = 4.

Die Nutzung des Stapelspeichers für rekursive Aufrufe ist in der Abbildung unten dargestellt.
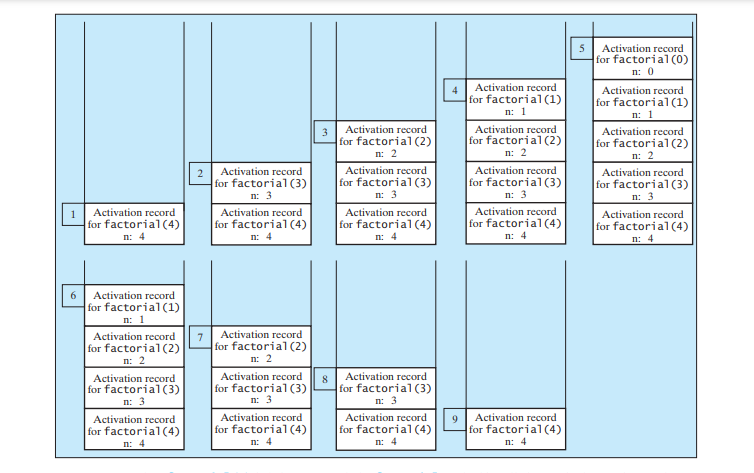
Es ist einfacher und effizienter, die Fakultätsmethode mithilfe einer Schleife zu implementieren. Allerdings verwenden wir hier die rekursive faktorielle-Methode, um das Konzept der Rekursion zu demonstrieren. Später in diesem Kapitel werden wir einige Probleme vorstellen, die von Natur aus rekursiv sind und ohne Verwendung der Rekursion schwer zu lösen sind.
Wenn die Rekursion das Problem nicht auf eine Weise reduziert, die es schließlich ermöglicht, in den Basisfall zu konvergieren, oder wenn kein Basisfall angegeben ist, kann es zu einer unendlichen Rekursion kommen. Angenommen, Sie schreiben die Methode Fakultät fälschlicherweise wie folgt:
öffentliche statische lange Fakultät (int n) {
return n * Faculty(n - 1);
}
Die Methode läuft unendlich und verursacht einen StackOverflowError.
Das in diesem Abschnitt besprochene Beispiel zeigt eine rekursive Methode, die sich selbst aufruft. Dies wird als direkte Rekursion bezeichnet. Es ist auch möglich, eine indirekte Rekursion zu erstellen. Dies tritt auf, wenn Methode A Methode B aufruft, die wiederum Methode A aufruft. An der Rekursion können sogar mehrere weitere Methoden beteiligt sein. Beispielsweise ruft Methode A Methode B auf, die Methode C aufruft, die wiederum Methode A aufruft.
Das obige ist der detaillierte Inhalt vonFallstudie: Berechnung von Fakultäten. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 So laden Sie Binance herunter
So laden Sie Binance herunter
 Der Unterschied zwischen Win7 32-Bit und 64-Bit
Der Unterschied zwischen Win7 32-Bit und 64-Bit
 So verwenden Sie die Shift-Hintertür
So verwenden Sie die Shift-Hintertür
 Welche anmeldefreien Plätze gibt es in China?
Welche anmeldefreien Plätze gibt es in China?
 vlookup gleicht zwei Datenspalten ab
vlookup gleicht zwei Datenspalten ab
 Lösung für fehlgeschlagene Verbindung zwischen wsus und Microsoft-Server
Lösung für fehlgeschlagene Verbindung zwischen wsus und Microsoft-Server
 Welche Videoformate gibt es?
Welche Videoformate gibt es?
 Waffenkammerkiste
Waffenkammerkiste




